Uncertainty, sampling error and confidence intervals

Lecture 3

Iain R. Moodie

BIOB11 - Experimental design and analysis for biologists

Department of Biology, Lund University

2025-03-31

Tree heights in a forest

Simulated population

Population \(N\) = 20000
Sample \(n\) = 100
- Trees sampled at random using a random number generator to provide coordinates
- Closest tree to that coordinate was measured

Tree heights in a forest

Simulated population and sample(s)

Tree heights in a forest

Simulated population and sample(s)

Worked example

Tree heights in a forest

Sample distribution

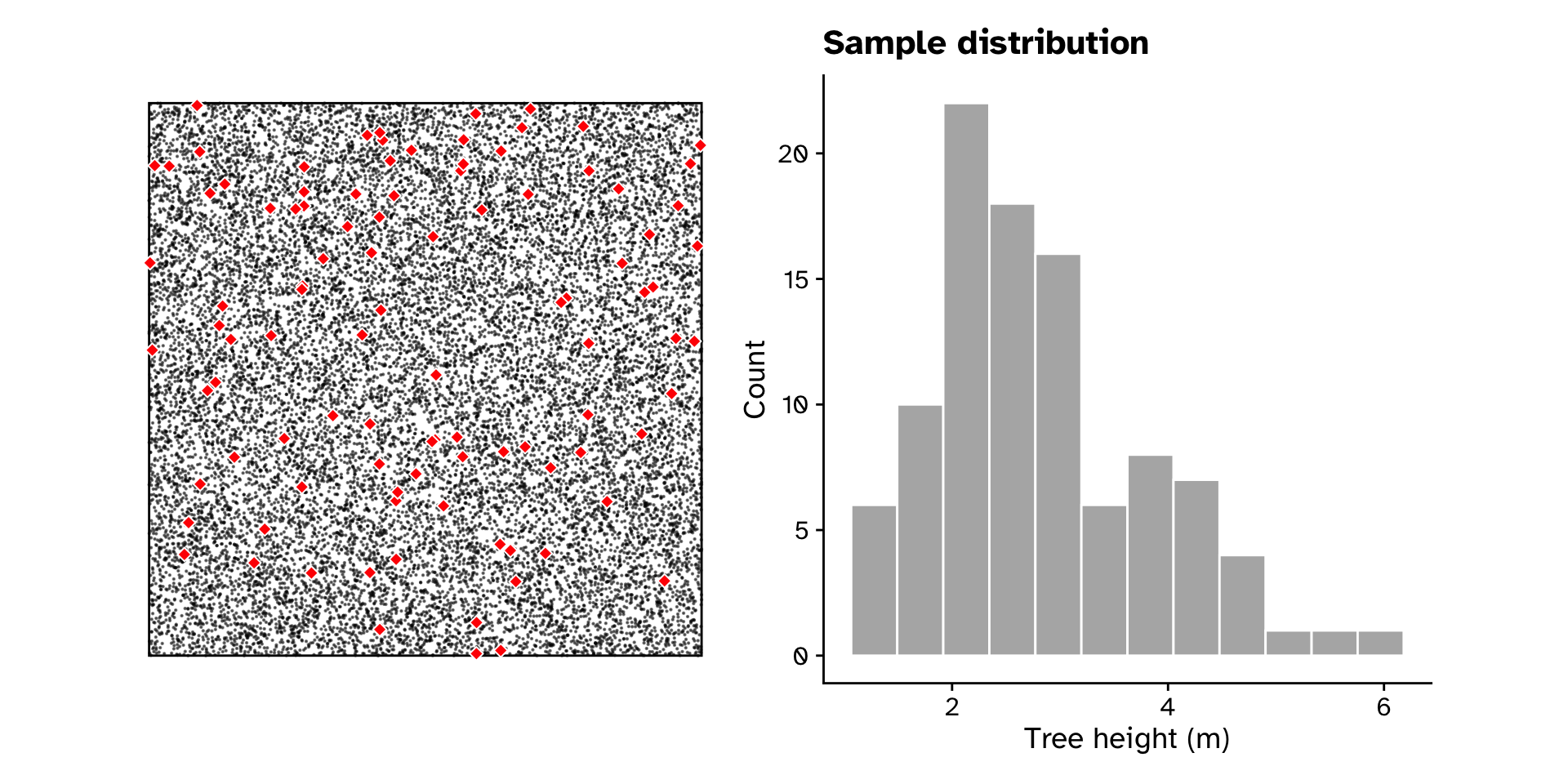
Tree heights in a forest

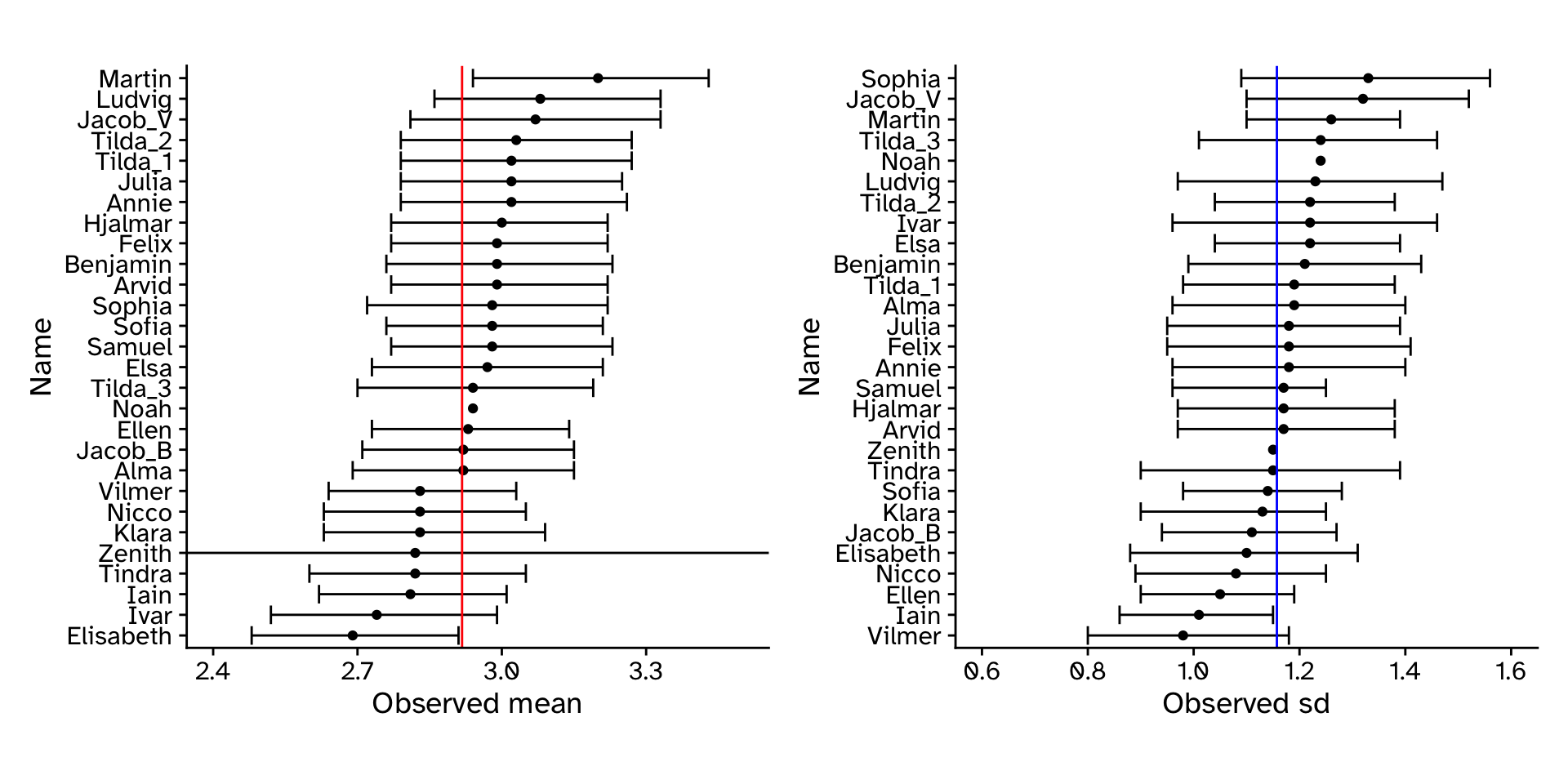
Observed statistics

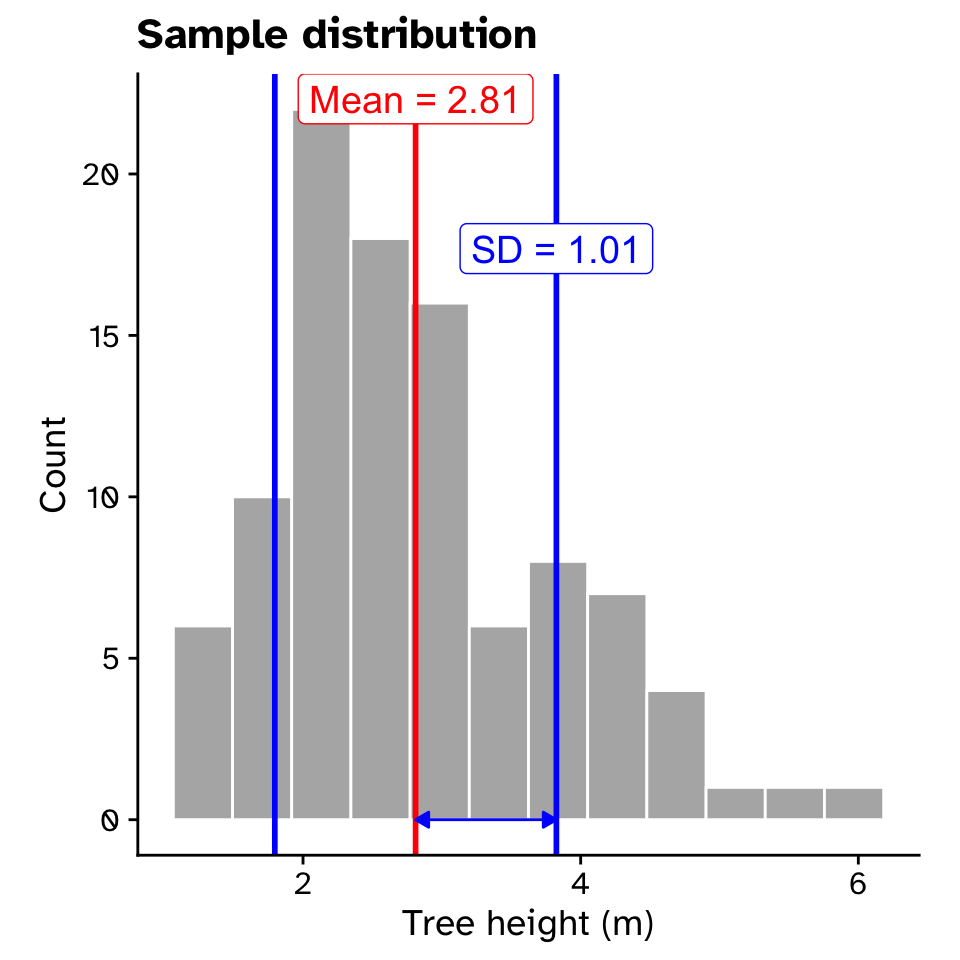
Tree heights in a forest

Uncertainty in our observed statistics

If we took another random sample of 100 trees, it is unlikely that we would get exactly the same observed statistics
We want to quantify this (sampling error)
Problem: we (usually) only ever collect one sample
Solution: generate more samples using information from our current sample

Tree heights in a forest

Generating a bootstrap sample

To generate more “samples”, we use a re-sampling technique called the “bootstrap”
- For original sample of size \(n\), sample \(n\) values with replacement many times
- There are \(n^n\) new samples we can generate from one sample
Important:
- the original sample must be representative of the population
- the original sample should be reasonably large (>>14, >30)

Tree heights in a forest

Generating a bootstrap sample

Tree heights in a forest

Generating a bootstrap sample

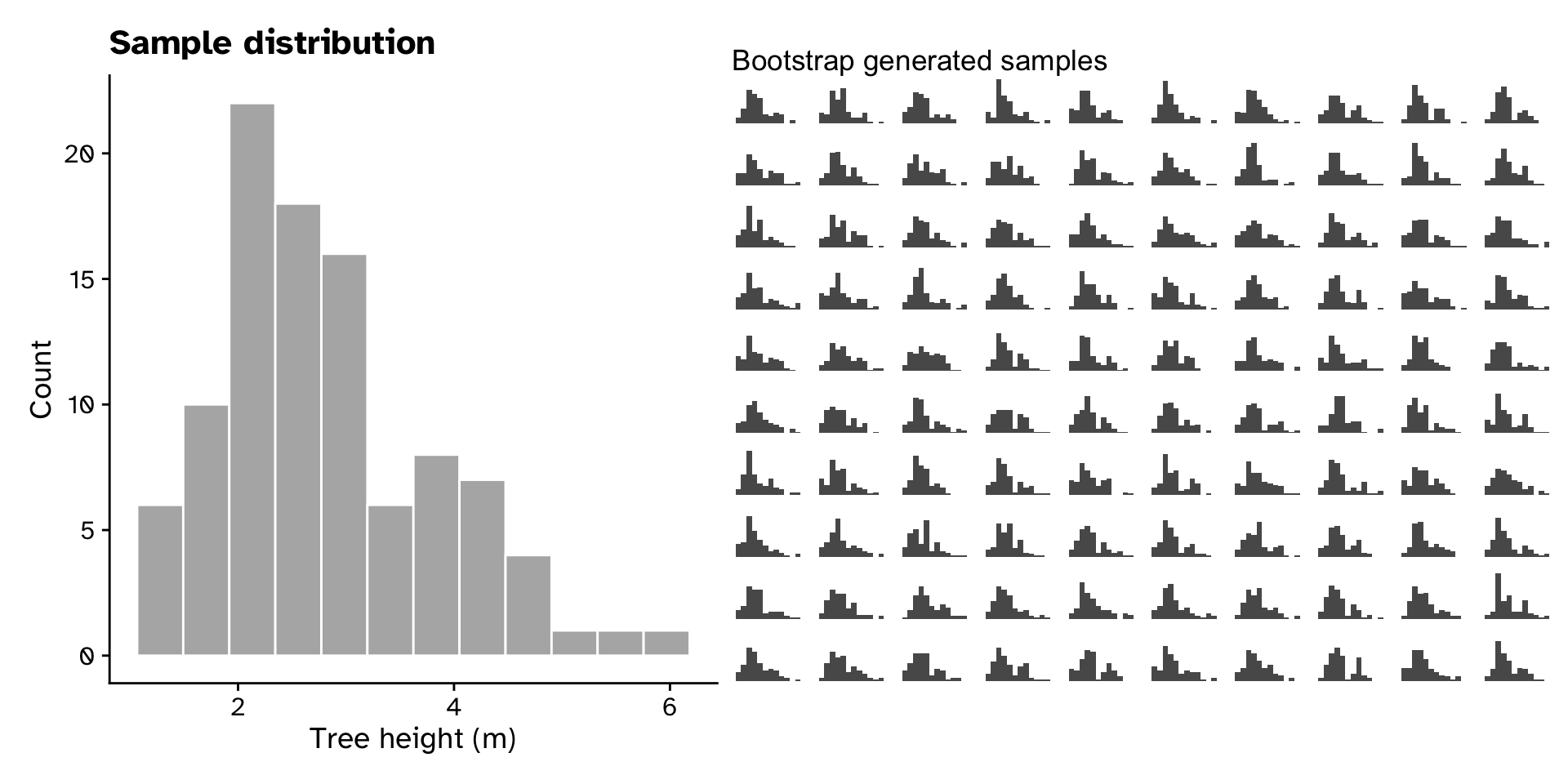
Tree heights in a forest

Calculate statistics from bootstrap sample

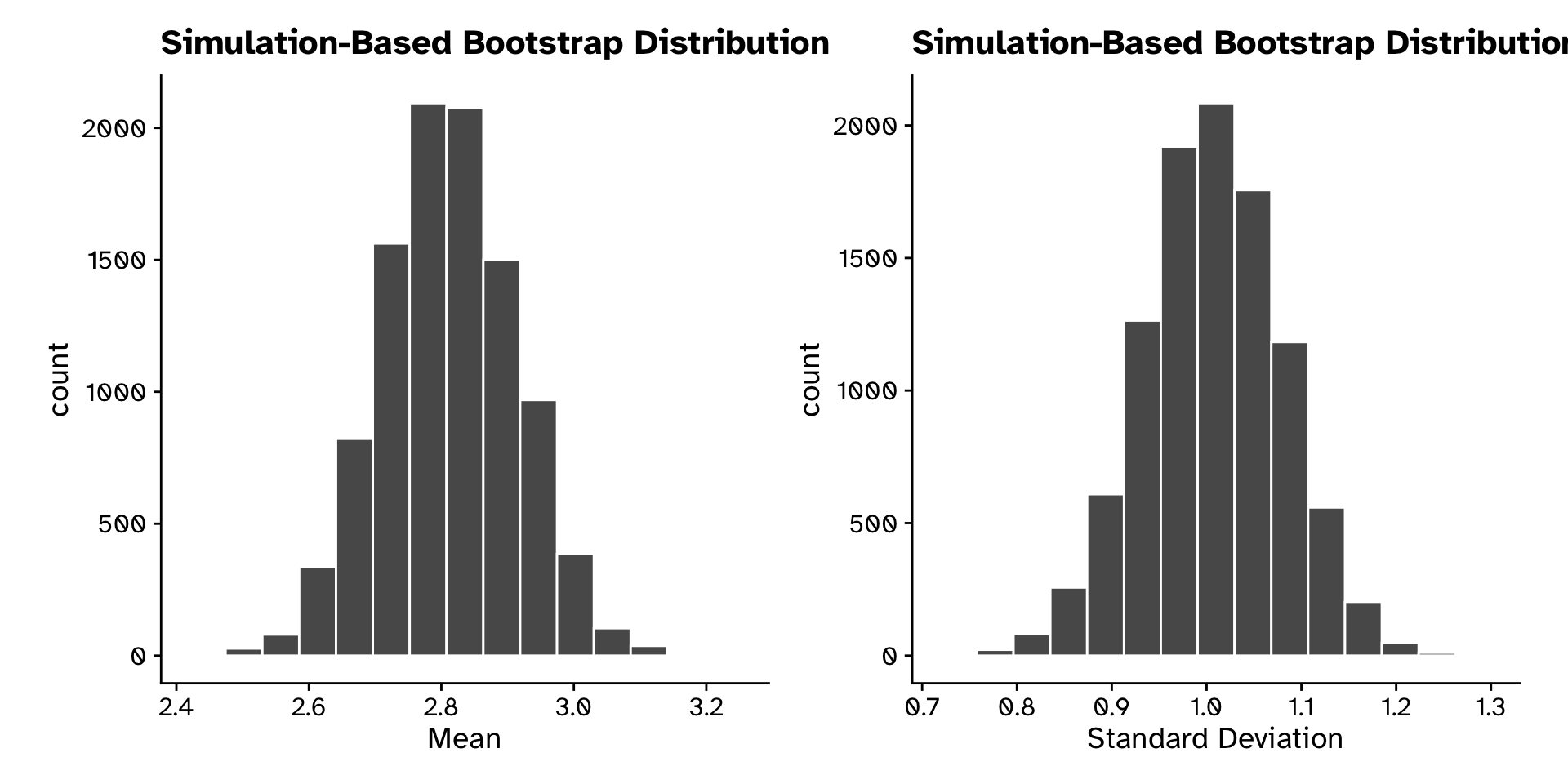
Tree heights in a forest

Calculate statistics from bootstrap sample

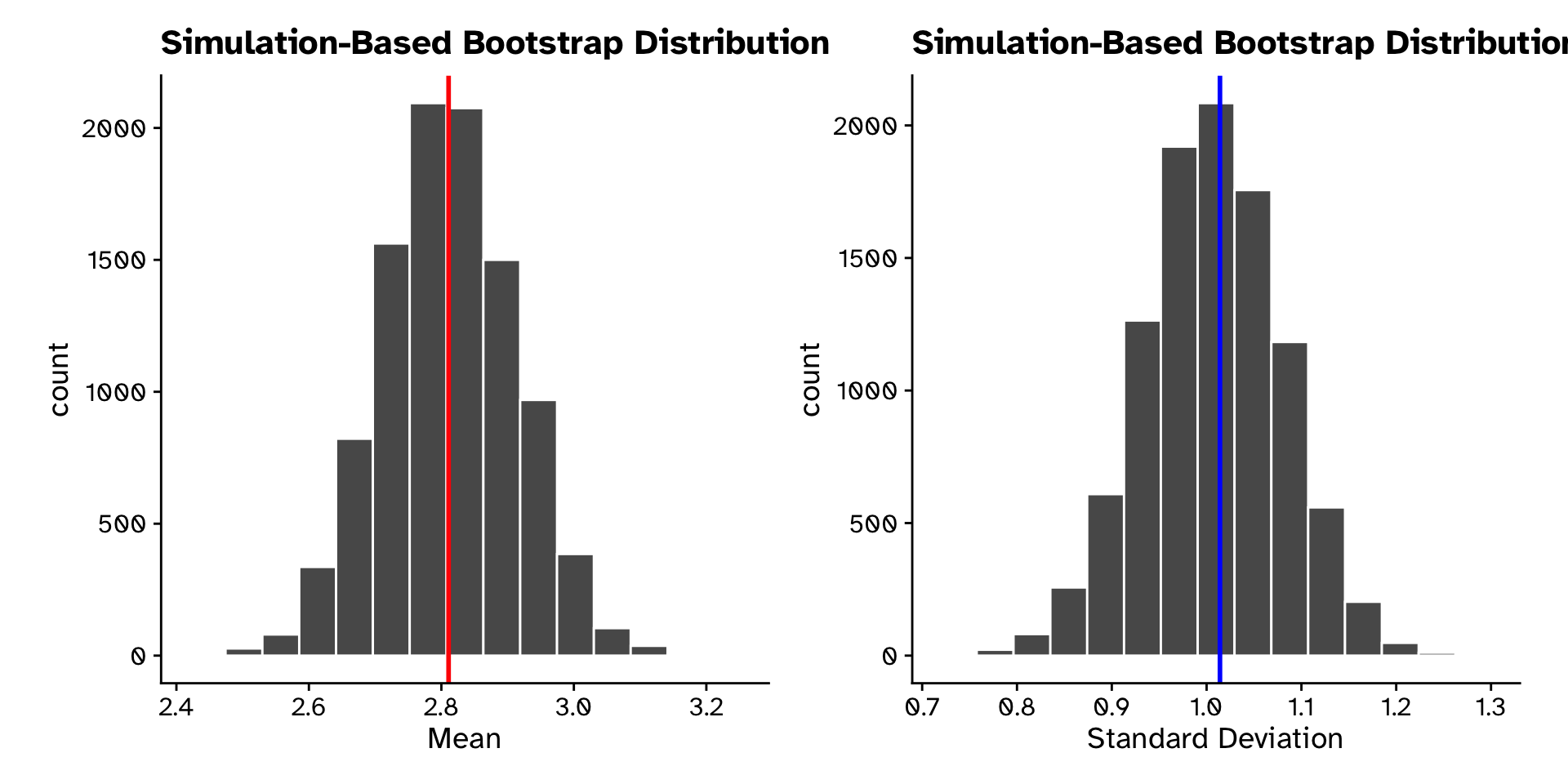
Tree heights in a forest

Use bootstrap sampling distribution to quanitify sampling error

Calculate the standard error (SE)
- Standard deviation of the sampling distribution
Calculate a confidence interval (CI)
- If we repeated our experiment many times and calculated a X% CI each time, the X% CI’s would include the “true” value X% of the time.
- SE method: Assume the sampling distribution is a normal distribution (bell-curve), and use a formula to find the values which contain the middle X% of the distribution (valid for means and some other statistics)
- Percentile method: The middle X% of the sampling distribution (valid for all statistics and shapes of sampling distributions*)

Tree heights in a forest

Calculate 95% CI from bootstrap sampling distribution

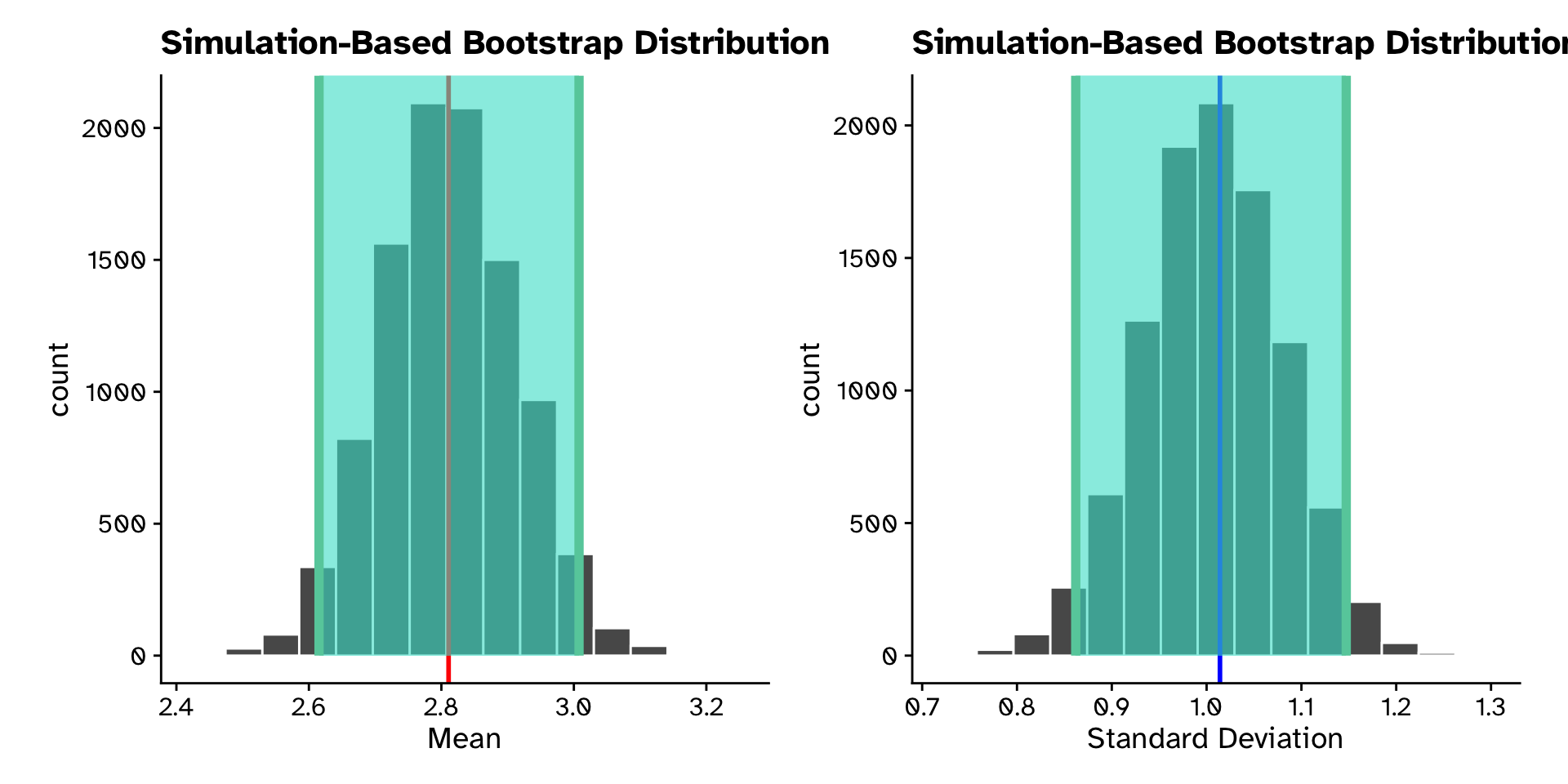
Tree heights in a forest

Calculate 95% CI from bootstrap sampling distribution

bootstrap_sample <-
  sample_trees |>
  specify(response = tree_height_m) |>
  generate(reps = 10000, type = "bootstrap")

bootstrap_sample |>
  calculate(stat = "mean") |>
  get_confidence_interval(type = "percentile")

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     2.62     3.01

bootstrap_sample |>
  calculate(stat = "sd") |>
  get_confidence_interval(type = "percentile")

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    0.862     1.15

Tree heights in a forest

Unusual scenario: we have multiple samples

Tree heights in a forest

Unusual scenario: we know the populations true parameters

Tree heights in a forest

How well did our approach work?

From single sample (usual scenario):
- Calculate observed statistics
- Generate bootstrap samples to create a sampling distribution
- Calculate 95% CI from bootstrap sampling distribution
From multiple samples:
- Calculate observed statistics
- Make a sampling distribution from observed statistics in each sample
- Use that sampling distribution to calculate 95% CI
Compare with population actual parameters

Tree heights in a forest

How well did our approach work?

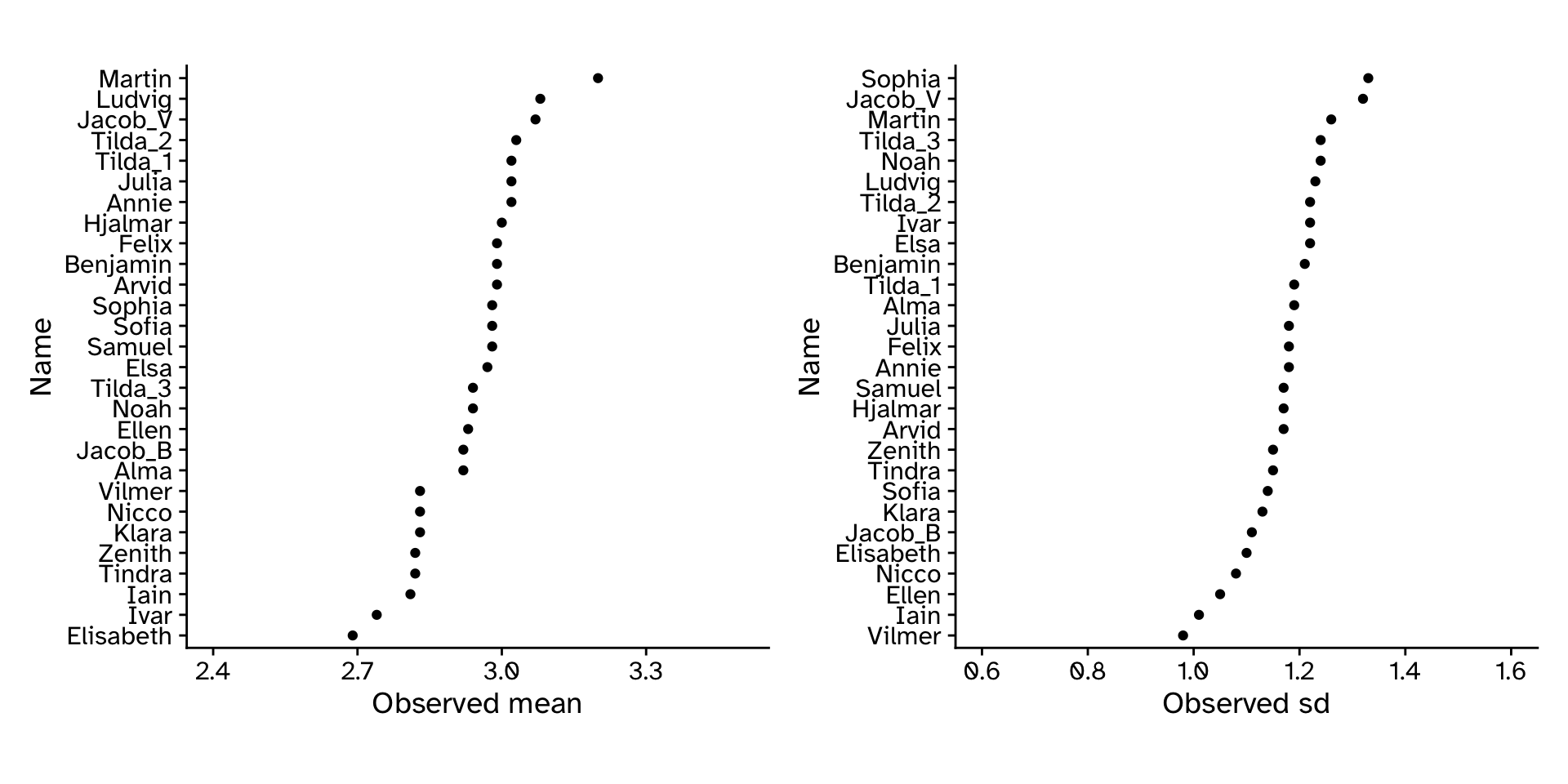
Tree heights in a forest

How well did our approach work?

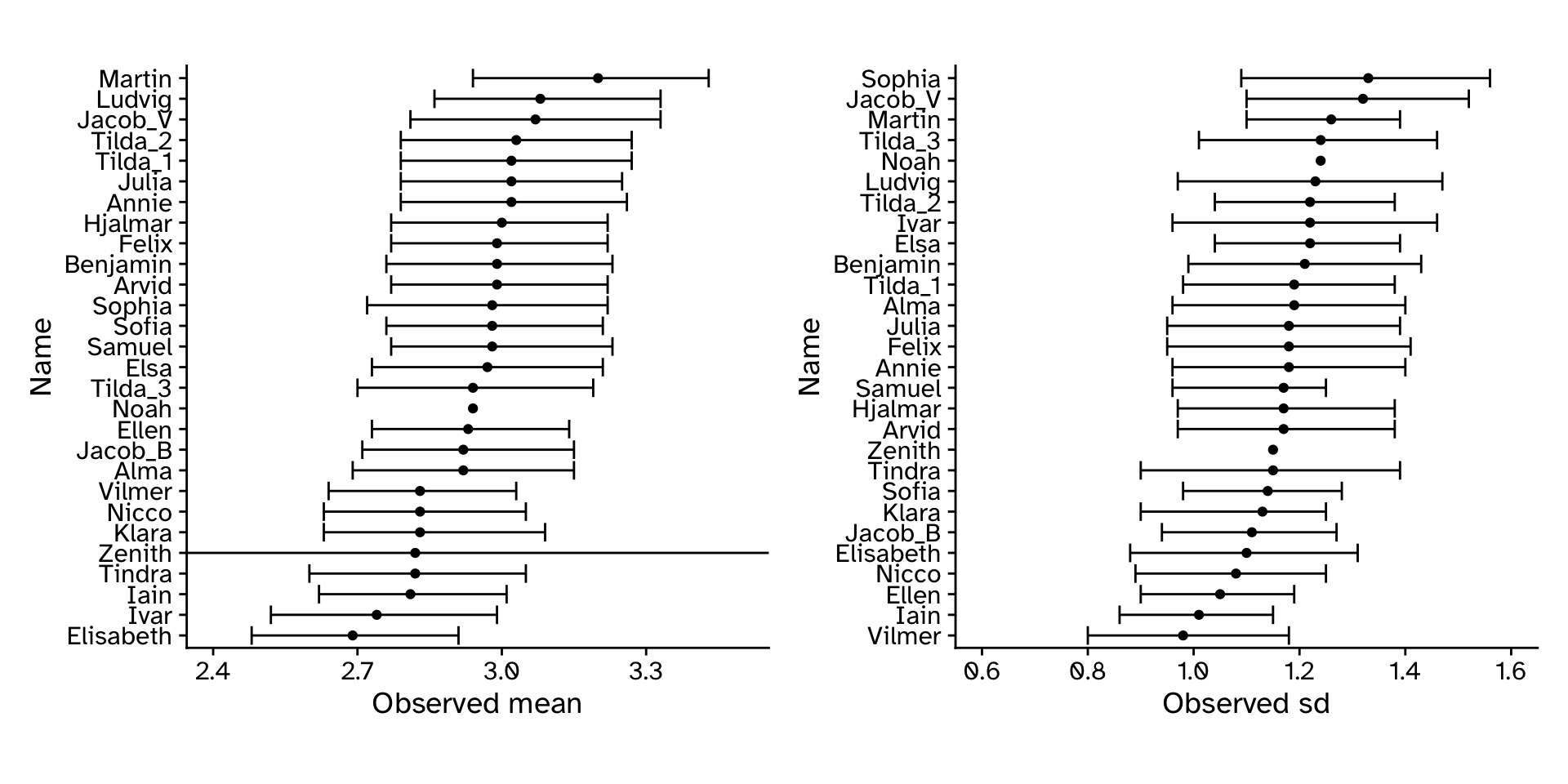
Tree heights in a forest

How well did our approach work?

CI: If we repeated our experiment many times and calculated a 95% CI each time, the 95% CI’s would include the “true” value 95% of the time.

Tree heights in a forest

How well did our approach work?

Confidence intervals

General workflow:

Get observed statistics:

specify() response (and explanatory) variable(s)
calculate() observed statistic

Get CI:

specify() response (and explanatory) variable(s)
generate() bootstrap samples
calculate() observed statistic in each sample
get_confidence_interval()

Confidence intervals

Examples: mean

iris_data <-
  iris |>
  filter(Species == "setosa")

iris_data |>
  specify(response = Petal.Width) |>
  calculate(stat = "mean")

Response: Petal.Width (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1 0.246

iris_data |>
  specify(response = Petal.Width) |>
  generate(reps = 10000, type = "bootstrap") |>
  calculate(stat = "mean") |>
  get_confidence_interval(type = "percentile")

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    0.218    0.276

Confidence intervals

Examples: difference in means

iris_data <-
  iris |>
  filter(Species == "setosa" | Species == "versicolor")

iris_data |>
  specify(response = Petal.Width, explanatory = Species) |>
  calculate(stat = "diff in means", order = c("setosa", "versicolor"))

Response: Petal.Width (numeric)
Explanatory: Species (factor)
# A tibble: 1 × 1
   stat
  <dbl>
1 -1.08

iris_data |>
  specify(response = Petal.Width, explanatory = Species) |>
  generate(reps = 10000, type = "bootstrap") |>
  calculate(stat = "diff in means", order = c("setosa", "versicolor")) |>
  get_confidence_interval(type = "percentile")

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    -1.14    -1.02

Confidence intervals

Examples: correlation

iris_data <-
  iris |>
  filter(Species == "setosa")

iris_data |>
  specify(response = Petal.Width, explanatory = Petal.Length) |>
  calculate(stat = "correlation")

Response: Petal.Width (numeric)
Explanatory: Petal.Length (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1 0.332

iris_data |>
  specify(response = Petal.Width, explanatory = Petal.Length) |>
  generate(reps = 10000, type = "bootstrap") |>
  calculate(stat = "correlation") |>
  get_confidence_interval(type = "percentile")

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1   0.0842    0.535