Theory based statistics (when sample sizes are small)

Lecture 5

Iain R. Moodie

BIOB11 - Experimental design and analysis for biologists

Department of Biology, Lund University

2025-04-01

There is only one test - Allen Downey

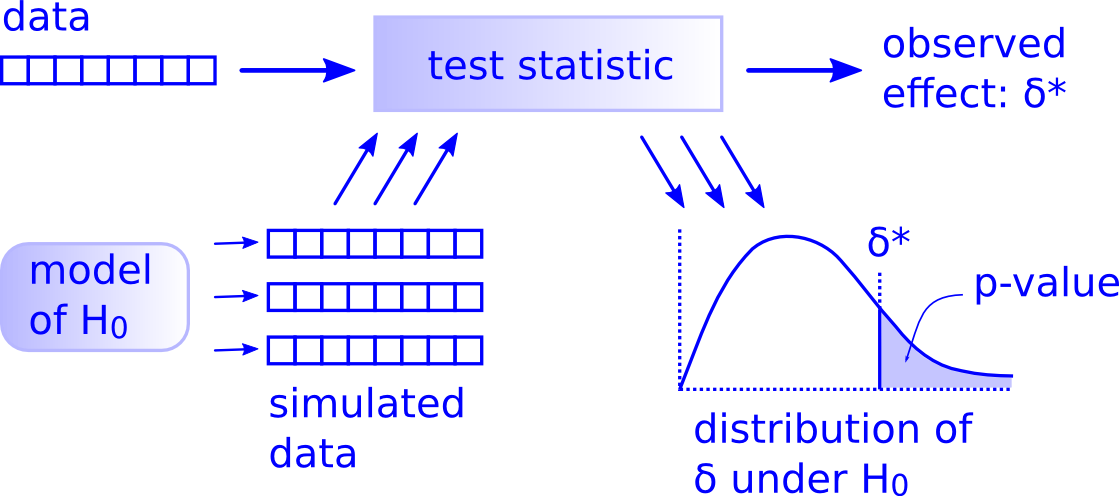
Re-sampling vs theory based statistics

Differences

Re-sampling:
- Relies on computational methods such as bootstrapping or permutation tests
- Does not require strict assumptions about the population distribution
- Uses the observed data to generate a sampling distribution
- Often computationally intensive

Re-sampling vs theory based statistics

Differences

Theory-based statistics:
- Relies on mathematical models and assumptions (e.g., normality, independence)
- Uses theoretical distributions to approximate the sampling distribution
- Requires smaller computational effort compared to re-sampling
- Assumptions must be met for valid results*

Re-sampling vs theory based statistics

What we have done and the theory based alternatives

Is a mean different from a point value?
- 1 sample t-test (1 sample sign test)
Are the means of two independant groups different from each other?
- 2 sample t-test (Mann-Whitney U test)
Are the means of two paired groups different from each other?
- paired sample t-test (Wilcoxon matched pairs test)
Are the means of three or more groups different from each other?
- one-way ANOVA (Kruskal-Wallis test)
Is there a relationship between two categorical variables?
- Chi-square test
Does a proportion differ from a point value?
- 1 prop sample test

There is only one test - Allen Downey

Re-sampling vs theory based statistics

Is a mean number of hours worked by a PhD student greater than 40?

data

# A tibble: 62 × 1
   hours_worked
          <dbl>
 1         37.6
 2         40  
 3         40.5
 4         40  
 5         39.9
 6         34.1
 7         40  
 8         34.8
 9         47.8
10         39.3
# ℹ 52 more rows

Re-sampling vs theory based statistics

Is a mean number of hours worked by a PhD student greater than 40?

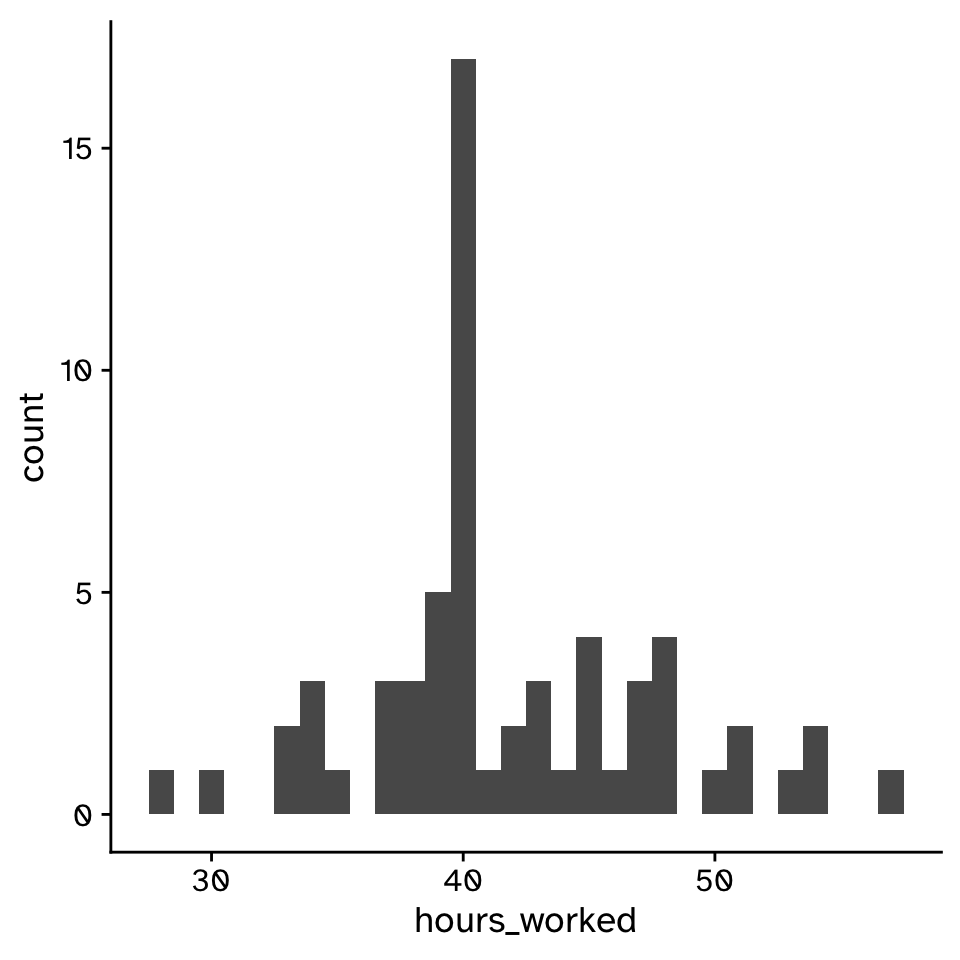
Re-sampling vs theory based statistics

Is a mean number of hours worked by a PhD student greater than 40?

Null hypothesis
- The mean number of hours worked is not different from 40
Alternative hypothesis
- The mean number of hours worked is greater than 40

Re-sampling vs theory based statistics

Resampling approach

observed_mean <- 
  data |>
  specify(response = hours_worked) |>
  calculate(stat = "mean")

observed_mean

Response: hours_worked (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  41.8

Re-sampling vs theory based statistics

Resampling approach

null_dist_resample <- 
  data |>
  specify(response = hours_worked) |>
  hypothesize(null = "point", mu = 40) |>
  generate(reps = 10000, type = "bootstrap") |>
  calculate(stat = "mean")

Re-sampling vs theory based statistics

Resampling approach

null_dist_resample |>
  visualize() +
  shade_p_value(observed_mean, direction = "greater")

Re-sampling vs theory based statistics

Resampling approach

p_value_resampling <- 
  null_dist_resample |>
  get_p_value(obs_stat = observed_mean, direction = "greater")

p_value_resampling

# A tibble: 1 × 1
  p_value
    <dbl>
1  0.0082

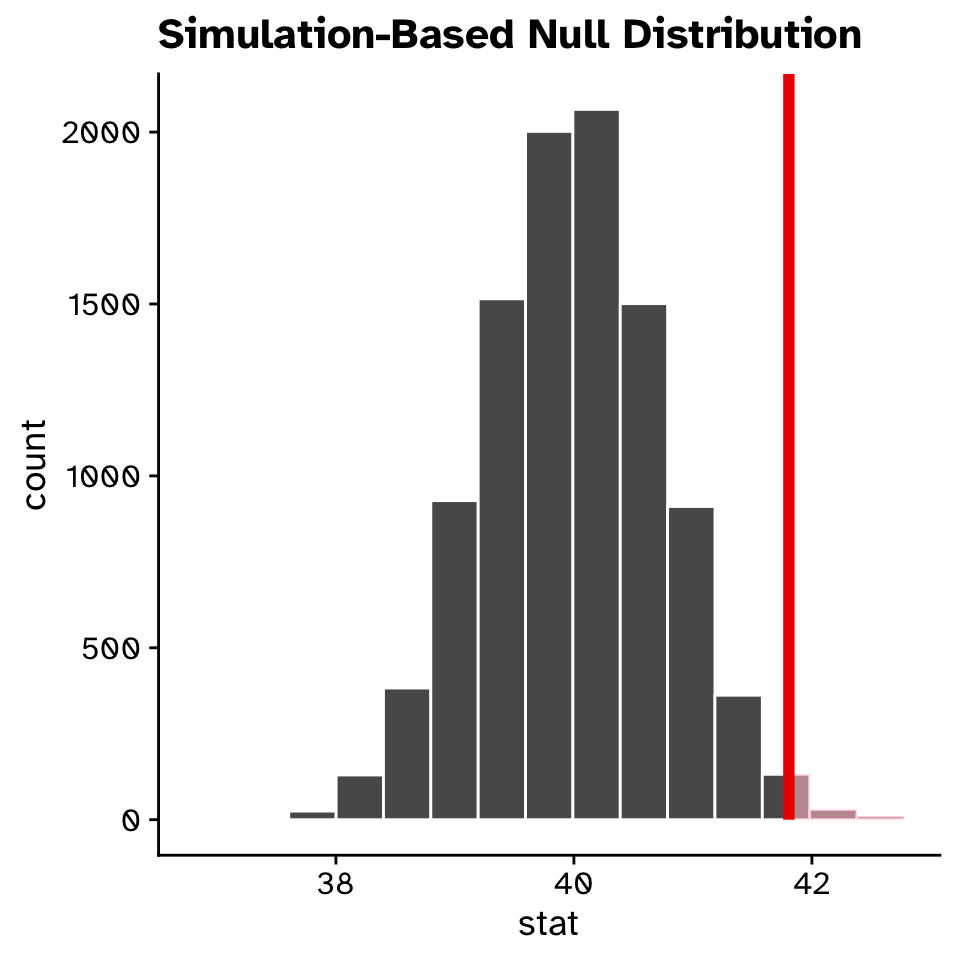
Re-sampling vs theory based statistics

Resampling approach

If the true mean number of hours worked per week was really 40, our approximation of the probability that we would see a test statistic as or more extreme than 41.8 is approximately 0.0082.

Re-sampling vs theory based statistics

Theory approach (1 sample t-test)

\[ t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} \]

observed_t <- 
  data |>
  specify(response = hours_worked) |>
  hypothesize(null = "point", mu = 40) |>
  calculate(stat = "t")

observed_t

Response: hours_worked (numeric)
Null Hypothesis: point
# A tibble: 1 × 1
   stat
  <dbl>
1  2.42

Re-sampling vs theory based statistics

Theory approach (1 sample t-test)

null_theory <-
  data |>
  specify(response = hours_worked) |>
  hypothesize(null = "point", mu = 40) |>
  assume(distribution = "t")

Re-sampling vs theory based statistics

Theory approach (1 sample t-test)

visualize(null_theory) +
  shade_p_value(observed_t, direction = "greater")

Re-sampling vs theory based statistics

Theory approach (1 sample t-test)

p_value_theory <- get_p_value(null_theory, observed_t, direction = "greater")
p_value_theory

# A tibble: 1 × 1
  p_value
    <dbl>
1 0.00935

p_value_resampling

# A tibble: 1 × 1
  p_value
    <dbl>
1  0.0082

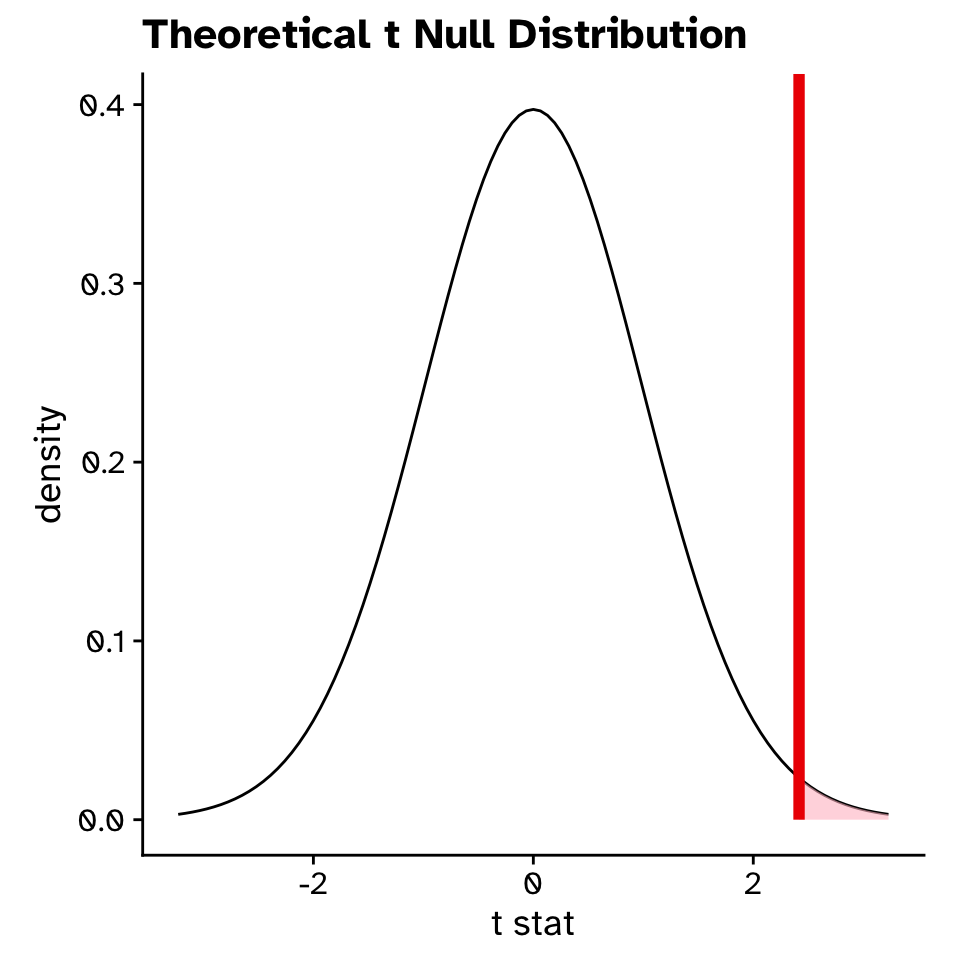
Re-sampling vs theory based statistics

Comparison

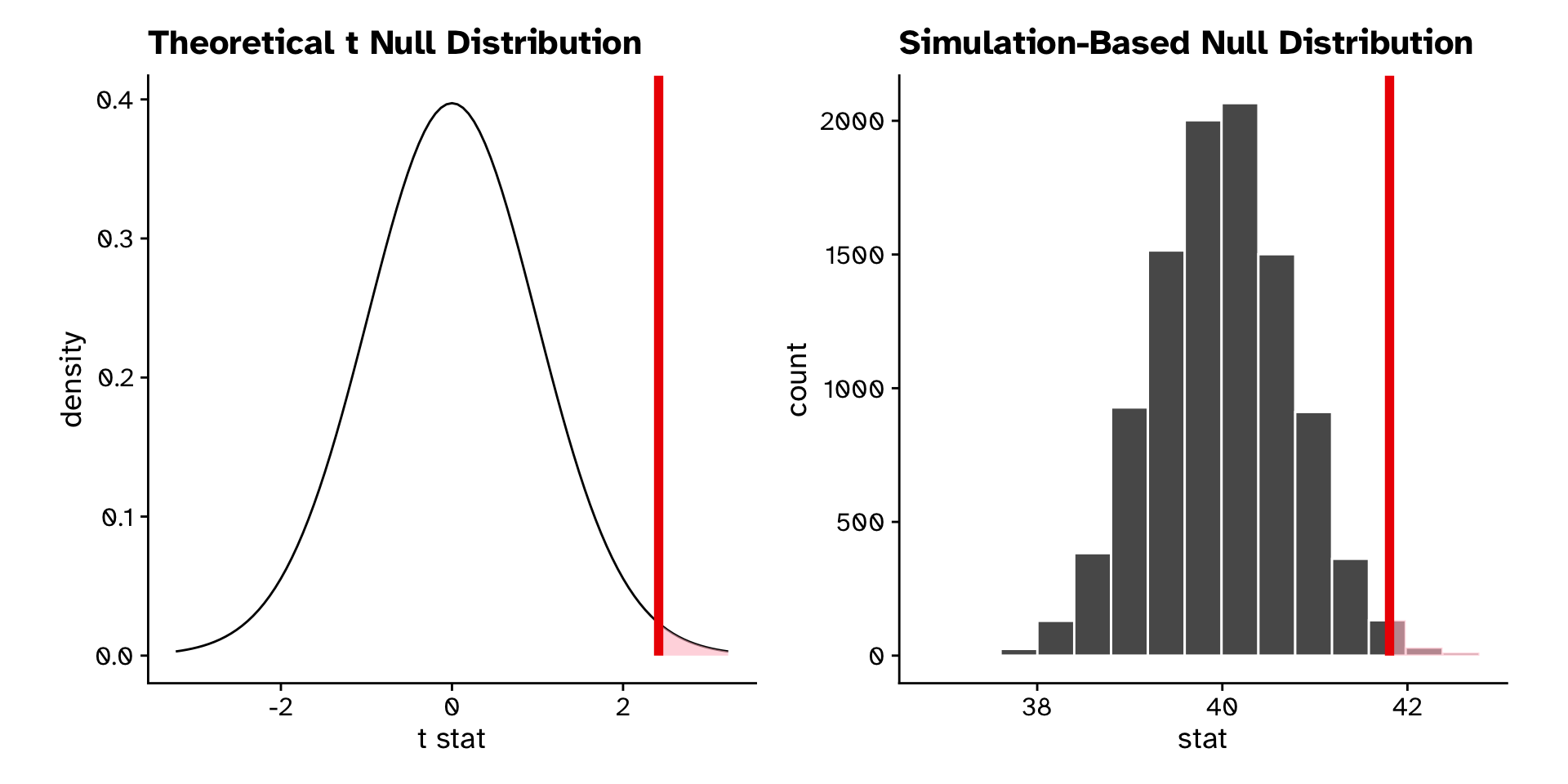
Re-sampling vs theory based statistics

Which to use?

Theory
- Makes assumptions about the distribution of your sample (often normal dist., equal variances)
- A way of adding extra information in (especially when sample sizes are small)
- Extremely quick to calculate

Re-sampling vs theory based statistics

Which to use?

Resampling
- Makes less assumptions about the distribution of your sample (not always a good thing!)
- Only information about the true distribution of the data can come from the sample
- Requires larger sample sizes to be accurate
- Takes longer to calculate

Re-sampling vs theory based statistics

What unites them?

Your sample is representative of the population you want to make inferences about
Collecting more data is always going to lead to more accurate inferences
Neither are magic
- Garbage in, garbage out
- Vunerable to “p-hacking” and other unethical uses