Test of and associations between categorical variables

Lecture 6

Iain R. Moodie

BIOB11 - Experimental design and analysis for biologists

Department of Biology, Lund University

2025-04-02

Tests of proportion

Could a proportion have been observed under a null hypothesis?

Tests of proportion

Could a proportion have been observed under a null hypothesis?

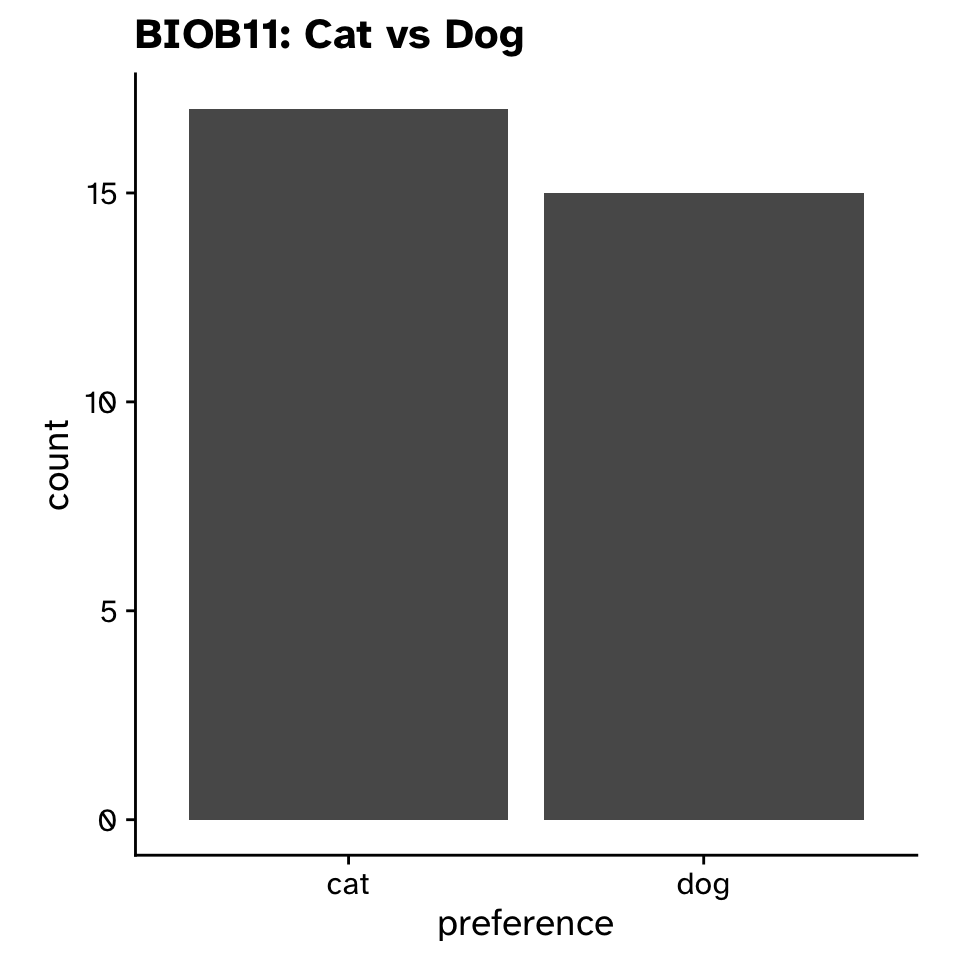
Tests of proportion

Could a proportion have been observed under a null hypothesis?

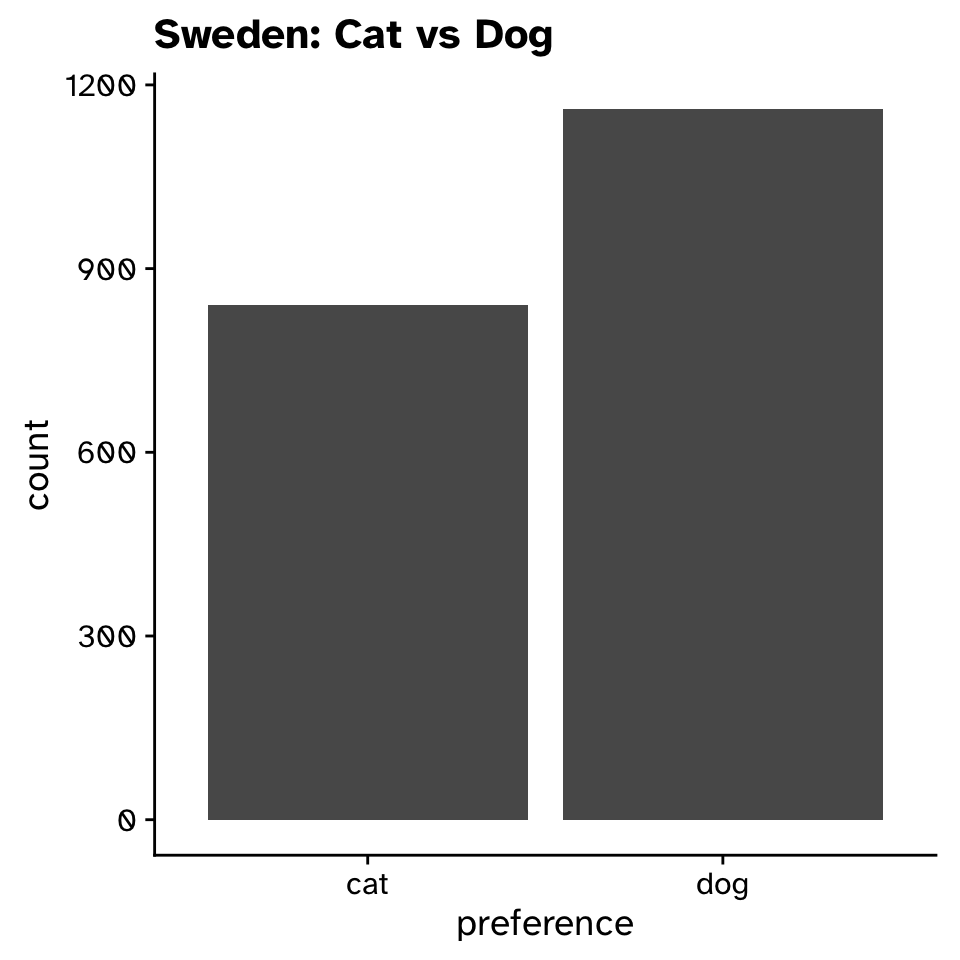
Tests of proportion

Could a proportion have been observed under a null hypothesis?

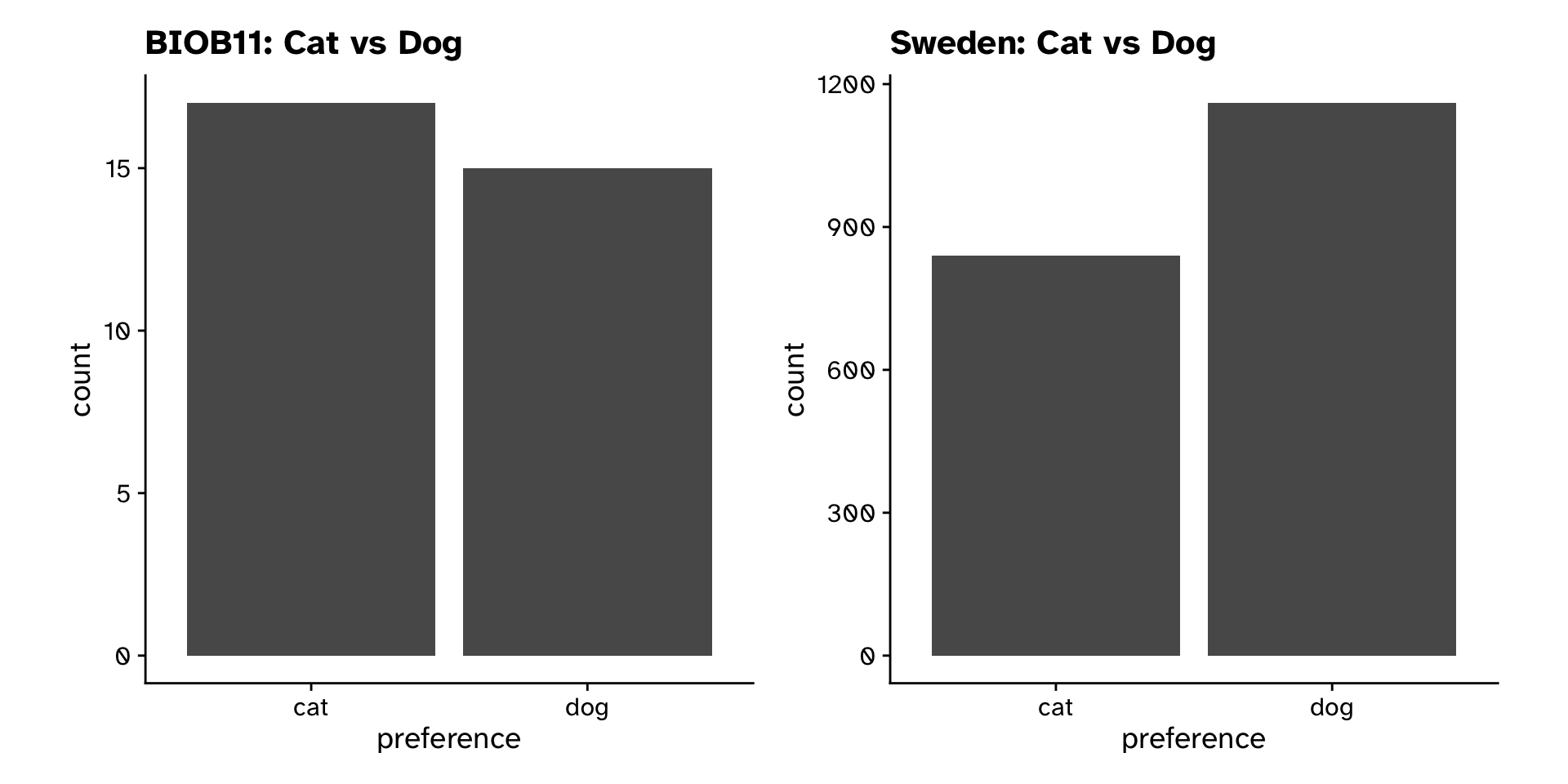
Tests of proportion

Could a proportion have been observed under a null hypothesis?

Null hypothesis:
- BIOB11 does not differ in their preference for cats vs dogs from the Swedish population
Alternative hypothesis:
- BIOB11 does differ in their preference for cats vs dogs from the Swedish population

Tests of proportion

Could a proportion have been observed under a null hypothesis?

animal_pref

# A tibble: 32 × 1
   preference
   <chr>     
 1 cat       
 2 dog       
 3 dog       
 4 dog       
 5 dog       
 6 cat       
 7 dog       
 8 dog       
 9 cat       
10 dog       
# ℹ 22 more rows

Tests of proportion

Could a proportion have been observed under a null hypothesis?

Calculate the test statistic:

observed_stat <- 
  animal_pref |>
  specify(response = preference, success = "dog") |>
  calculate(stat = "prop")

observed_stat

Response: preference (factor)
# A tibble: 1 × 1
   stat
  <dbl>
1 0.469

Tests of proportion

Could a proportion have been observed under a null hypothesis?

Generate a null distibution:

null_dist <- 
  animal_pref |>
  specify(response = preference, success = "dog") |>
  hypothesize(null = "point", p = 0.58) |>
  generate(reps = 20000, type = "draw") |>
  calculate(stat = "prop")

Tests of proportion

Could a proportion have been observed under a null hypothesis?

Visualise the null:

null_dist |>
  visualize(bins = 20) +
  shade_p_value(obs_stat = observed_stat, direction = "two-sided")

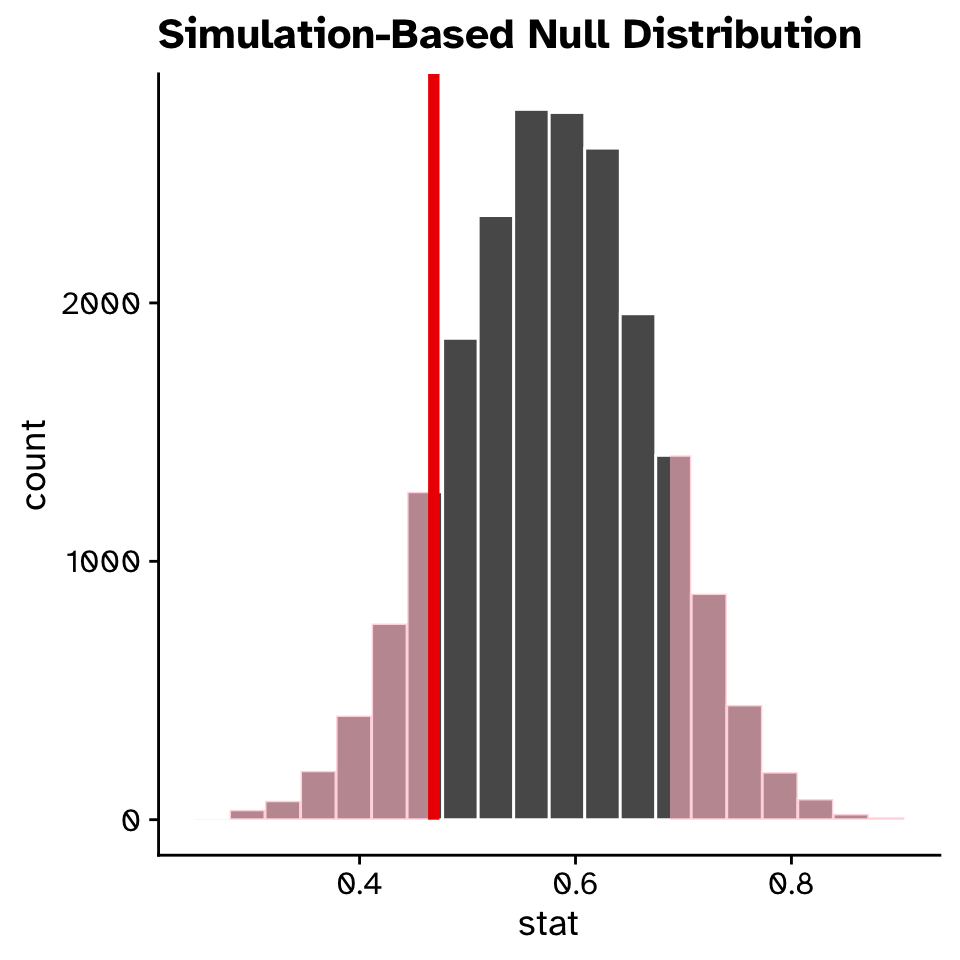
Tests of proportion

Could a proportion have been observed under a null hypothesis?

Calculate the p-value:

null_dist |>
  get_p_value(obs_stat = observed_stat, direction = "two-sided")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.273

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

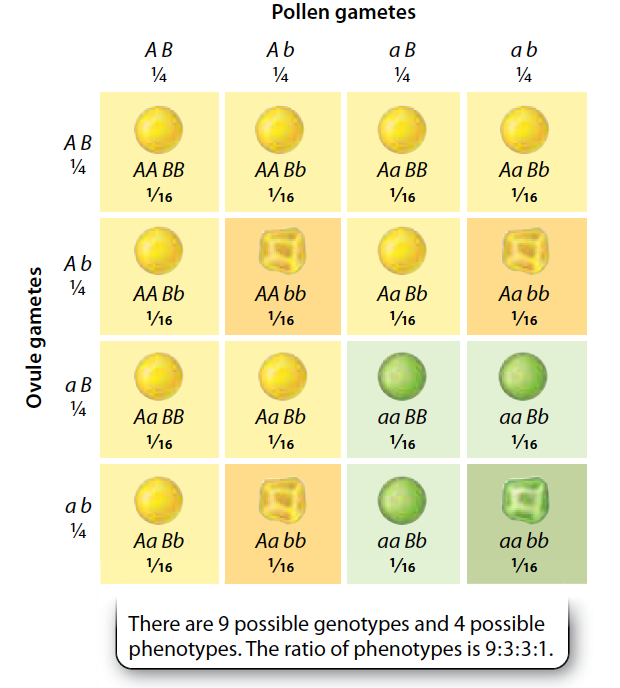
\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

Null hypothesis:
- The sample came from the hypothesised distribution
- The sample distribution is not different from the hypothesised distribution
Alternative hypotheis:
- The sample came from a different distribution to the one hypothesised
- The sample distribution is different from the hypothesised distribution

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

mendelian_data

# A tibble: 120 × 1
   phenotype
   <chr>    
 1 A-B-     
 2 A-B-     
 3 A-B-     
 4 A-B-     
 5 A-B-     
 6 A-B-     
 7 A-B-     
 8 A-B-     
 9 A-B-     
10 A-B-     
# ℹ 110 more rows

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

ggplot(mendelian_data, aes(x = phenotype)) +
  geom_bar() +
  geom_hline(yintercept = c(9, 3, 1)/16*nrow(mendelian_data), linetype = "dashed", color = "red")

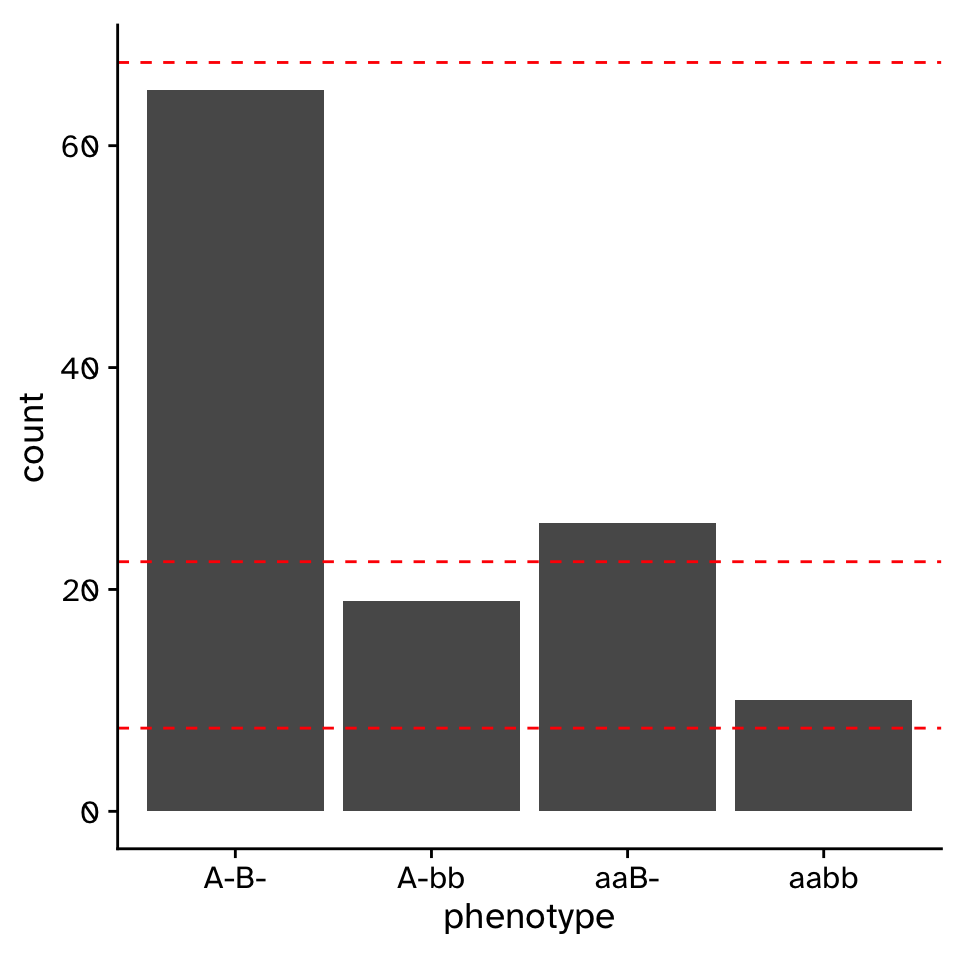
\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

\[ \chi^2 = \sum \frac{(Observed_i - Expected_i)^2}{Expected_i} \]

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

observed_statistic <- 
  mendelian_data |>
  specify(response = phenotype) |>
  hypothesize(
    null = "point",
    p = c(
      "A-B-" = 9/16,
      "A-bb" = 3/16,
      "aaB-" = 3/16,
      "aabb" = 1/16
    )
   ) |>
  calculate(stat = "Chisq")

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

null_dist <- 
  mendelian_data |>
  specify(response = phenotype) |>
  hypothesize(
    null = "point",
    p = c(
      "A-B-" = 9/16,
      "A-bb" = 3/16,
      "aaB-" = 3/16,
      "aabb" = 1/16
    )
   ) |>
  generate(reps = 10000, type = "draw") |>
  calculate(stat = "Chisq")

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

null_dist |>
  visualize() + 
  shade_p_value(observed_statistic, direction = "greater")

\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

null_dist |>
  get_p_value(obs_stat = observed_stat, direction = "greater")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.922

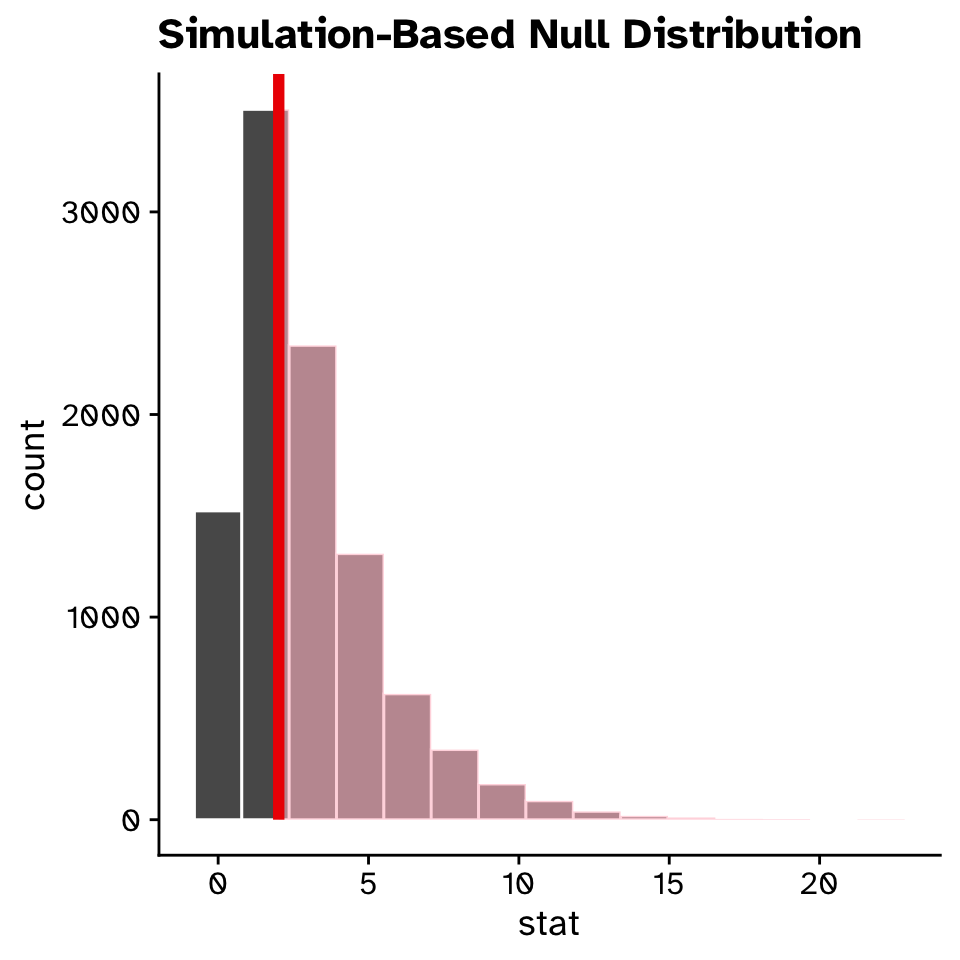
\(\chi^2\) Goodness of fit

Does the observed data differ from an expected distribution?

Fail to reject null hypothesis.
The distribution of phenotypes is compatible with mendelian inheritance.

\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

Null hypothesis:
- The two categorical variables are not associated with each other
- The two categorical variables are independent
Alternative hypothesis:
- The two categorical variables are associated with each other
- The two categorical variables are not independent

\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

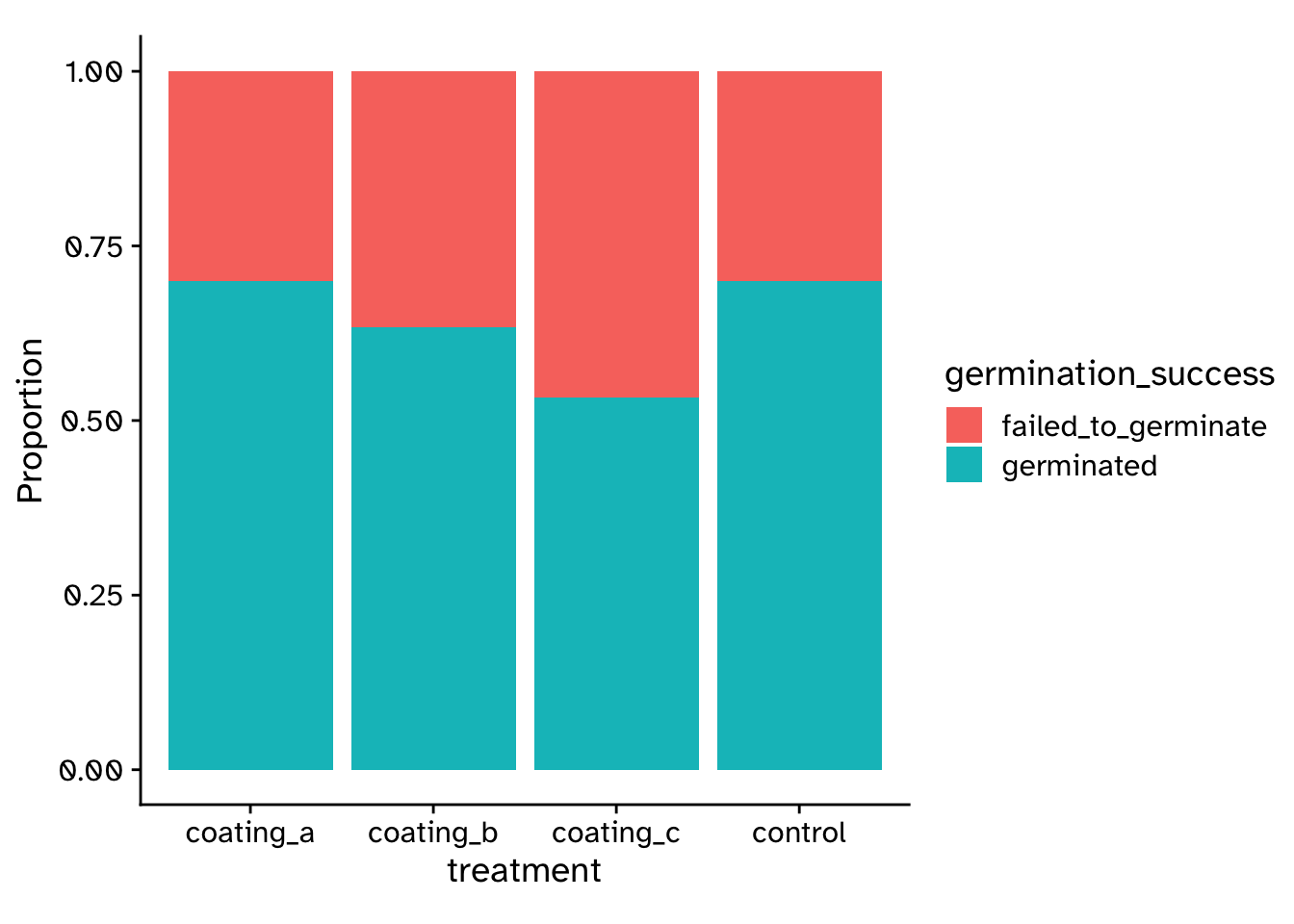
\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

germ_data

# A tibble: 120 × 2
   treatment germination_success
   <chr>     <chr>              
 1 coating_a germinated         
 2 coating_a germinated         
 3 coating_a germinated         
 4 coating_a failed_to_germinate
 5 coating_a germinated         
 6 coating_a germinated         
 7 coating_a germinated         
 8 coating_a germinated         
 9 coating_a germinated         
10 coating_a germinated         
# ℹ 110 more rows

\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

observed_statistic <- 
  germ_data |>
  specify(response = germination_success, explanatory = treatment) |>
  hypothesize(null = "independence") |>
  calculate(stat = "Chisq")

observed_statistic

Response: germination_success (factor)
Explanatory: treatment (factor)
Null Hypothesis: independence
# A tibble: 1 × 1
   stat
  <dbl>
1  2.43

\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

null_dist <- 
  germ_data |>
  specify(response = germination_success, explanatory = treatment) |>
  hypothesize(null = "independence") |>
  generate(reps = 10000, type = "permute") |>
  calculate(stat = "Chisq")

\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

null_dist |>
  visualize() +
  shade_p_value(observed_statistic, direction = "greater")

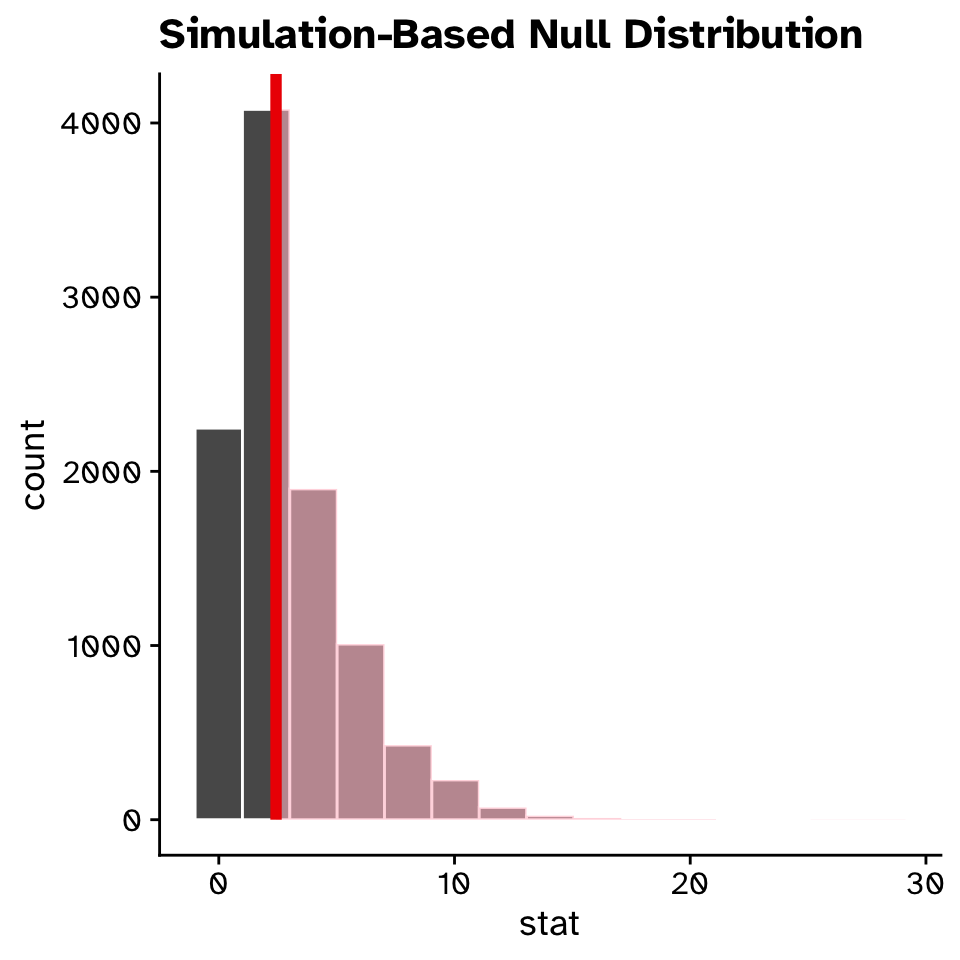
\(\chi^2\) Test of independence

Are two categorical variables associated with each other?

null_dist |>
  get_p_value(obs_stat = observed_stat, direction = "greater")

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.906