Correlation, Causation, and Linear Regression

Lecture 8

Iain R. Moodie

BIOB11 - Experimental design and analysis for biologists

Department of Biology, Lund University

2025-04-04

Correlation

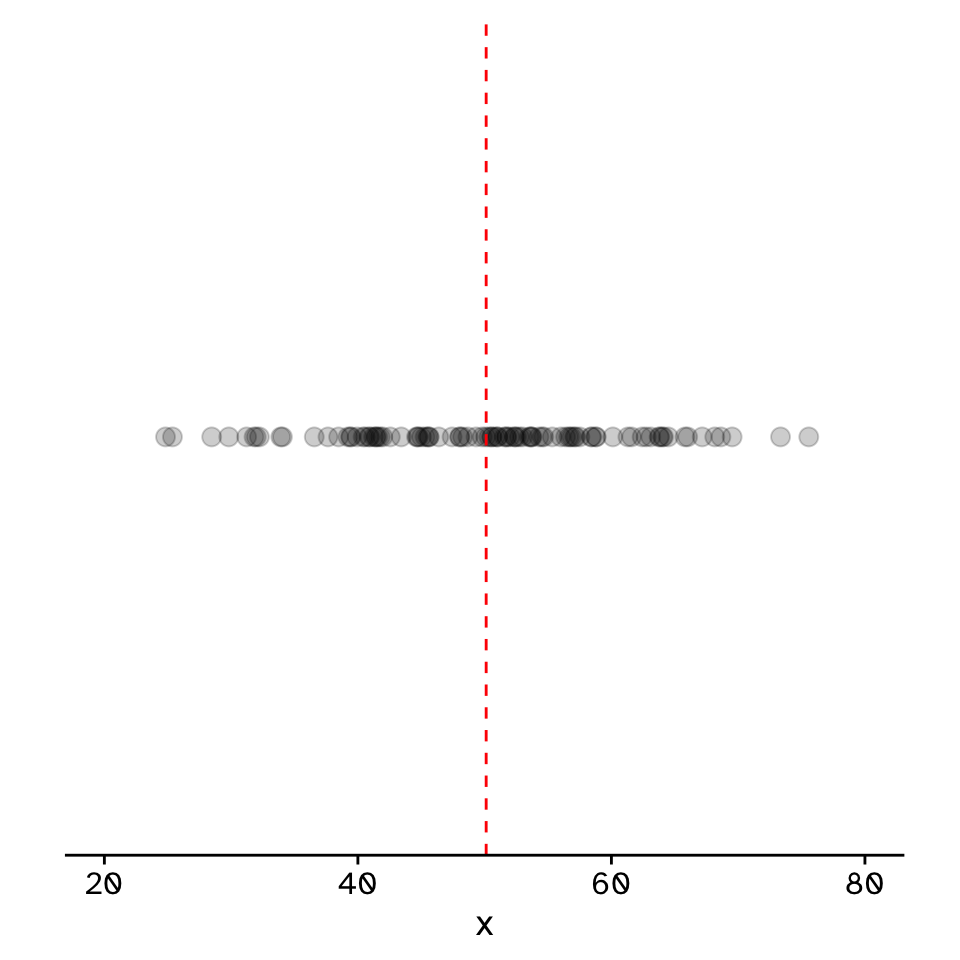
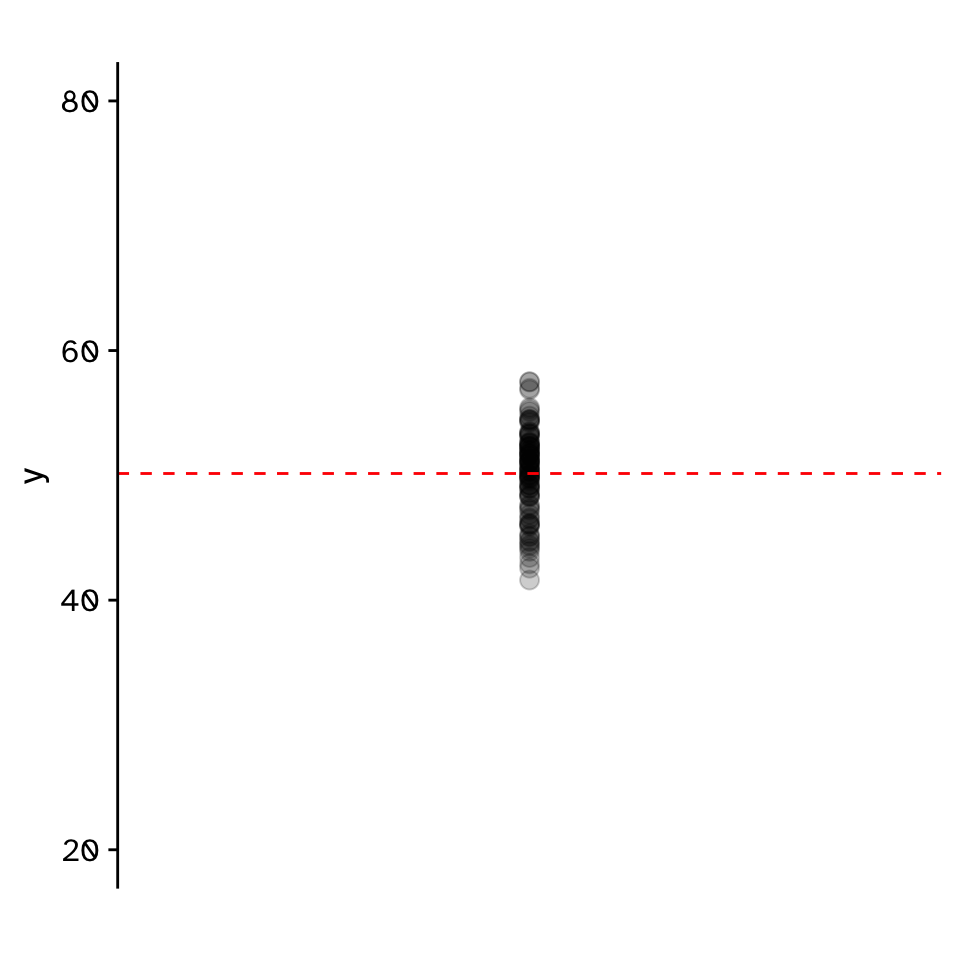
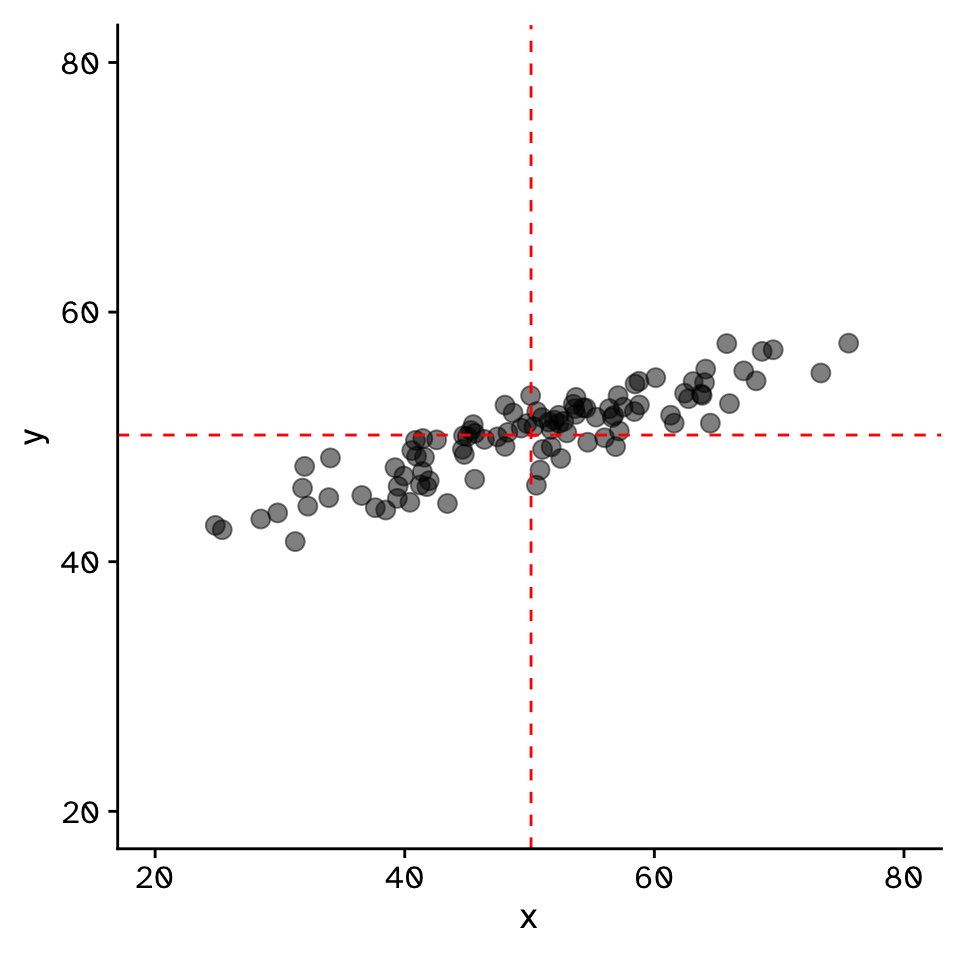
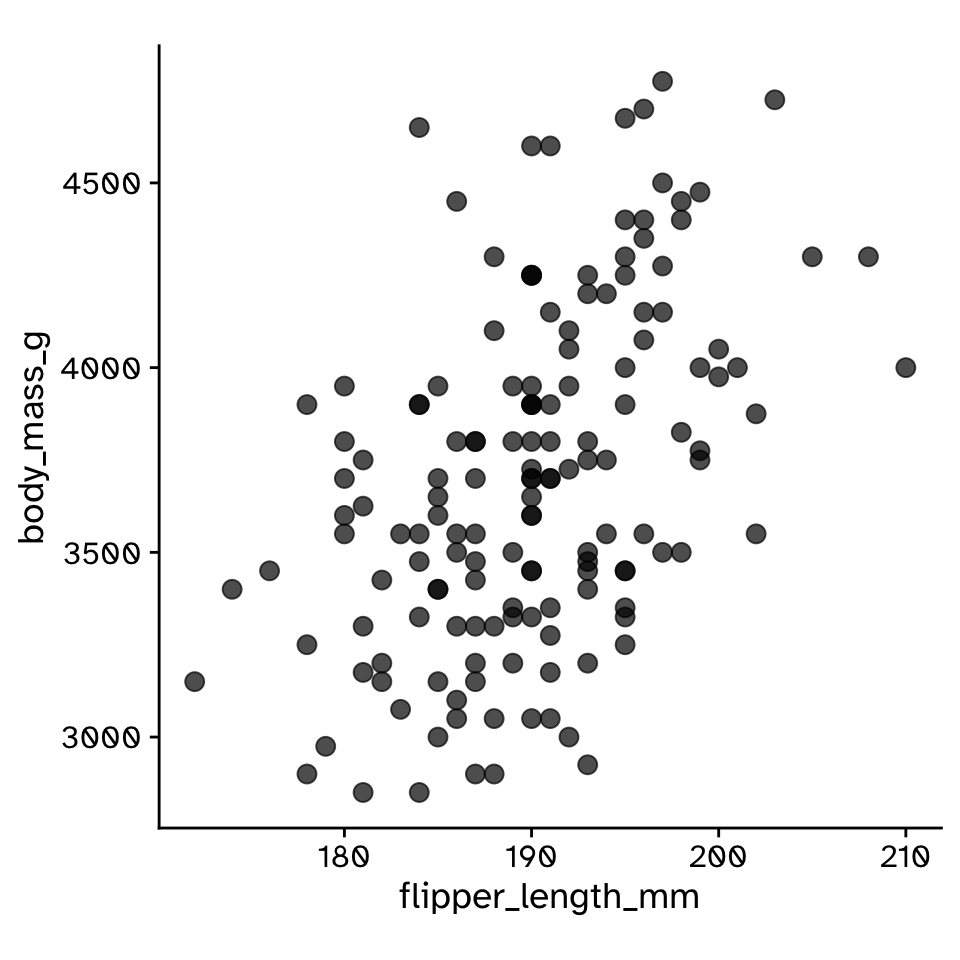
Do two continuous variables covary?

Used to assess if two continuous variables are independent, or if they covary (linearly)
We do not express one variable as a function of another:
- No “response” and “explanatory”
Usually assumed that both variables are “effects of a common cause” (Sokal and Rohlf 1995)
“Correlation does not mean causation”
- But you can measure a correlation between a cause and effect

Correlation

Do two continuous variables covary?

Correlation

Do two continuous variables covary?

Correlation coefficient (Pearson):

\[ r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}} \]

\[ r = \frac{\text{Covariance}(x,y)}{\text{Standard deviation}(x) \times \text{Standard deviation}(y)} \]

\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]

Correlation

Do two continuous variables covary?

\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]

Correlation

Do two continuous variables covary?

\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]

Calculate standard deviation in \(x\):

\[ \sigma_x = \sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \]

data |>
  observe(response = x, stat = "sd")

Response: x (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  10.9

Correlation

Do two continuous variables covary?

\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]

Calculate standard deviation in \(y\):

\[ \sigma_y = \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2} \]

data |>
  observe(response = y, stat = "sd")

Response: y (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  3.51

Correlation

Do two continuous variables covary?

\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]

Calculate the covariance between \(x\) and \(y\):

\[ Cov(x,y) = \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \]

data |>
  cov()

          x        y
x 118.23297 33.87468
y  33.87468 12.31625

Correlation

Do two continuous variables covary?

\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]

data |>
  specify(x ~ y) |>
  calculate(stat = "correlation")

Response: x (numeric)
Explanatory: y (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1 0.888

Correlation

Do two continuous variables covary?

Correlation

Do two continuous variables covary?

Correlation coefficient (\(r\)): \[ r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}} \]

Coefficient of determination (\(r^2\)): \[ r^2 = \left(\frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}}\right)^2 \]

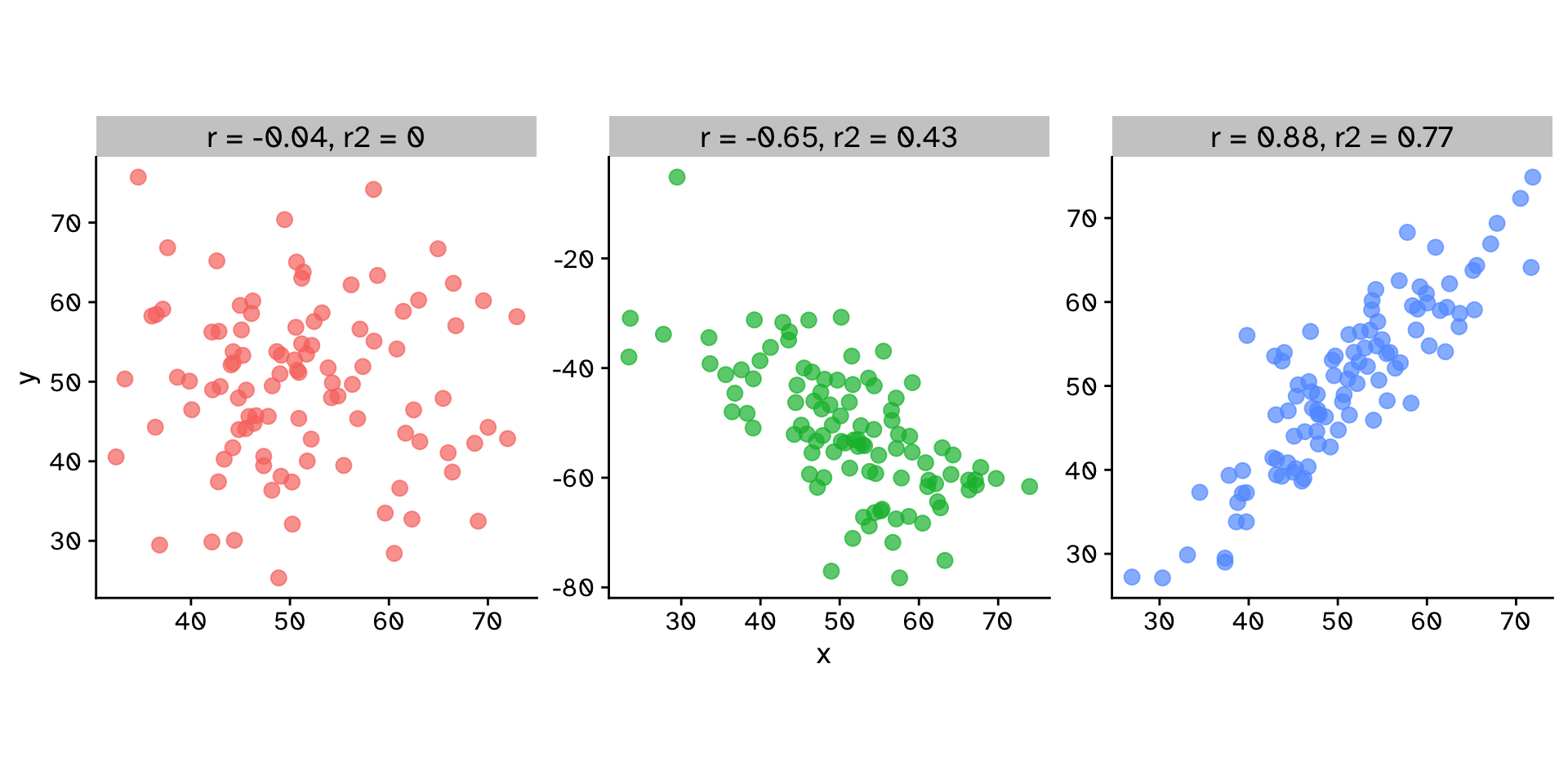
Correlation

Do two continuous variables covary?

Correlation

Do two continuous variables covary?

Correlation

Do two continuous variables covary?

adelie_data <-
  penguins |>
  filter(species == "Adelie")
  
adelie_data |>
  ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point(size = 3, alpha = 0.7)

Correlation

Observed statistic

observed_correlation <-
  adelie_data |>
  specify(flipper_length_mm ~ body_mass_g) |>
  calculate(stat = "correlation")

observed_correlation

Response: flipper_length_mm (numeric)
Explanatory: body_mass_g (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1 0.468

Correlation

Confidence intervals

boot_dist <-
  adelie_data |>
  specify(flipper_length_mm ~ body_mass_g) |>
  generate(reps = 10000, type = "bootstrap") |>
  calculate(stat = "correlation")

percentile_ci <- get_ci(boot_dist, type = "percentile")

Correlation

Confidence intervals

visualize(boot_dist) +
  shade_confidence_interval(endpoints = percentile_ci) +
  labs(x = "r")

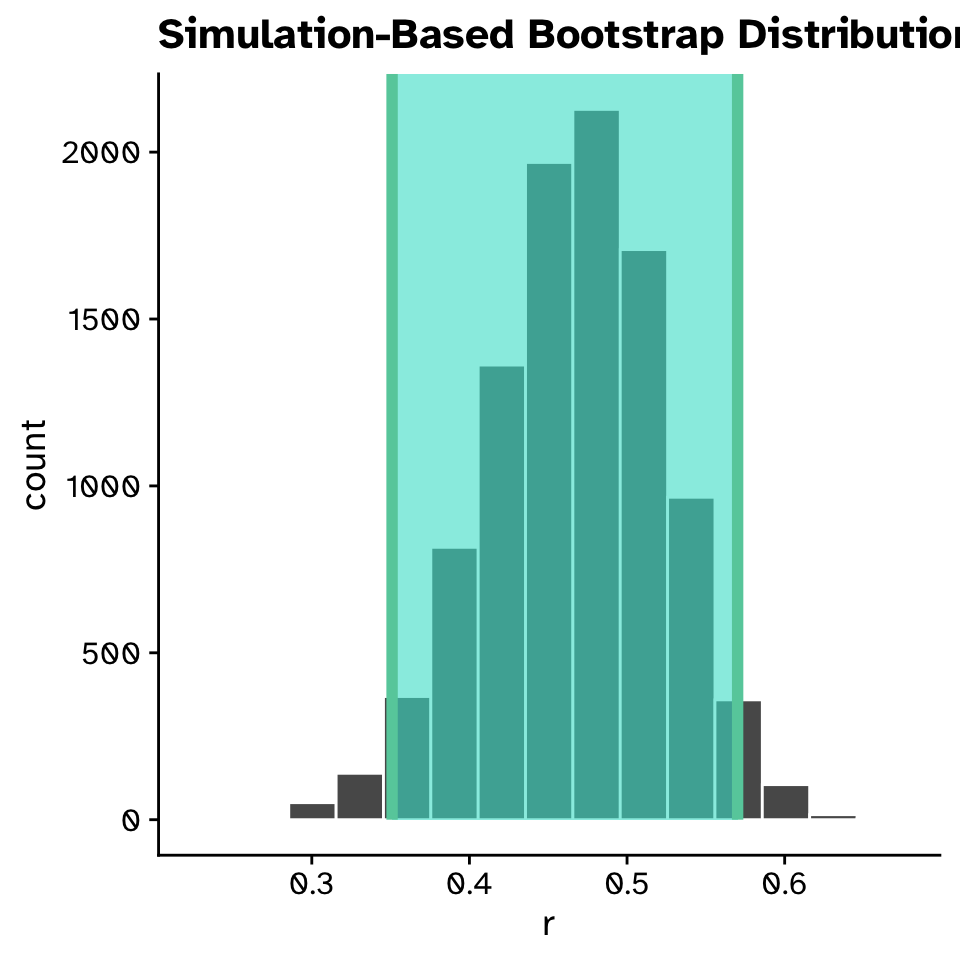
Correlation

Confidence intervals

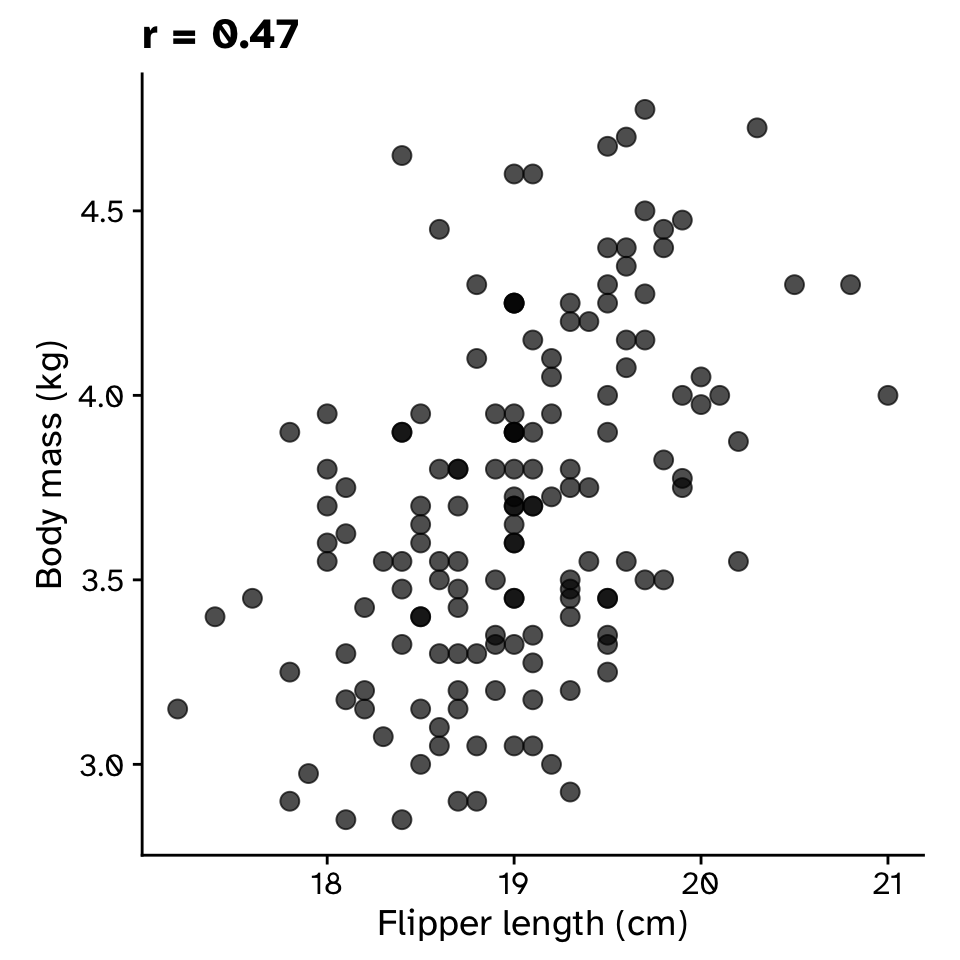
The correlation between flipper length and body mass was 0.468 (95% CI: 0.355, 0.572).

Correlation

Hypothesis test

Null hypothesis:
- The two variables do not covary (\(r=0\))
Alternative hypothesis:
- The two variables do covary (\(r\neq0\))

Correlation

Hypothesis test

How could we generate a null distribution?

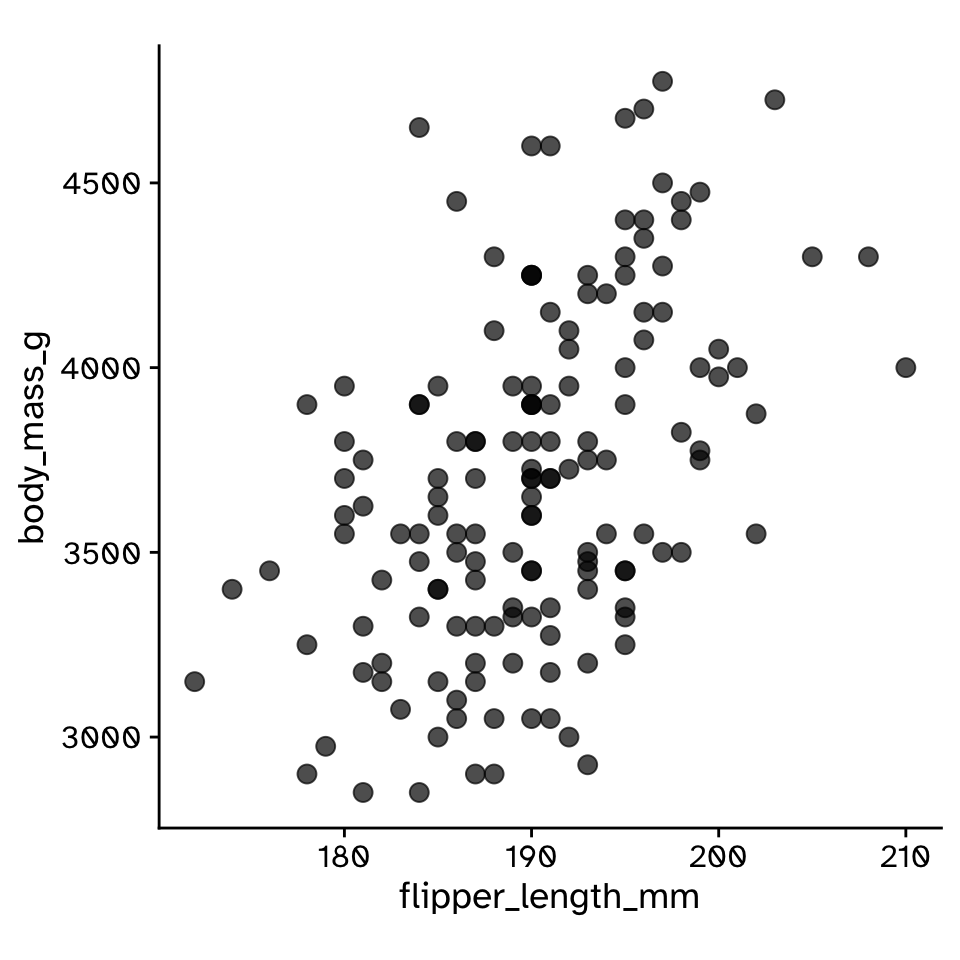
Correlation

Hypothesis test

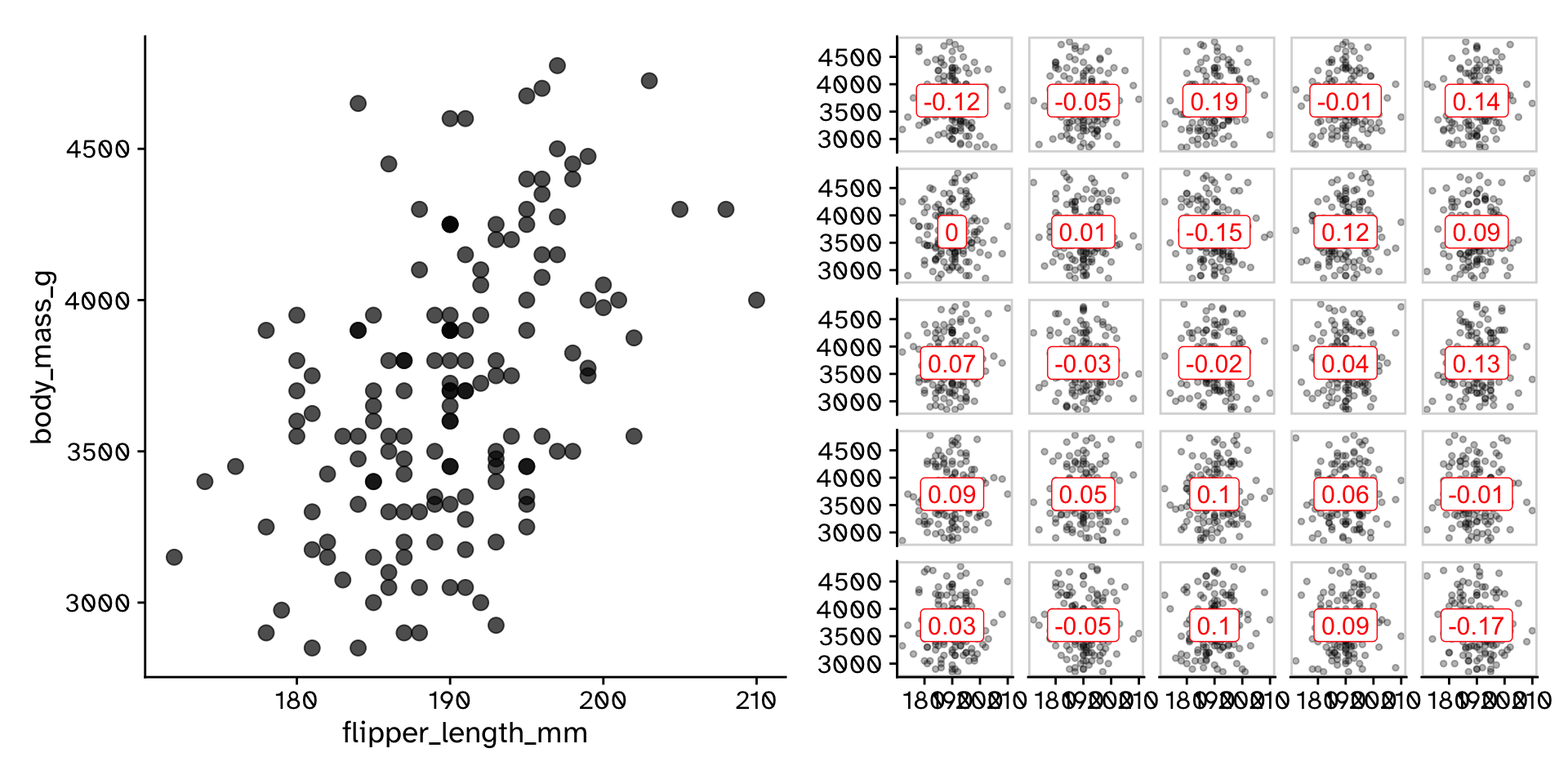
Correlation

Hypothesis test

null_dist <-
  adelie_data |>
  specify(flipper_length_mm ~ body_mass_g) |>
  hypothesize(null = "independence") |>
  generate(reps = 10000, type = "permute") |>
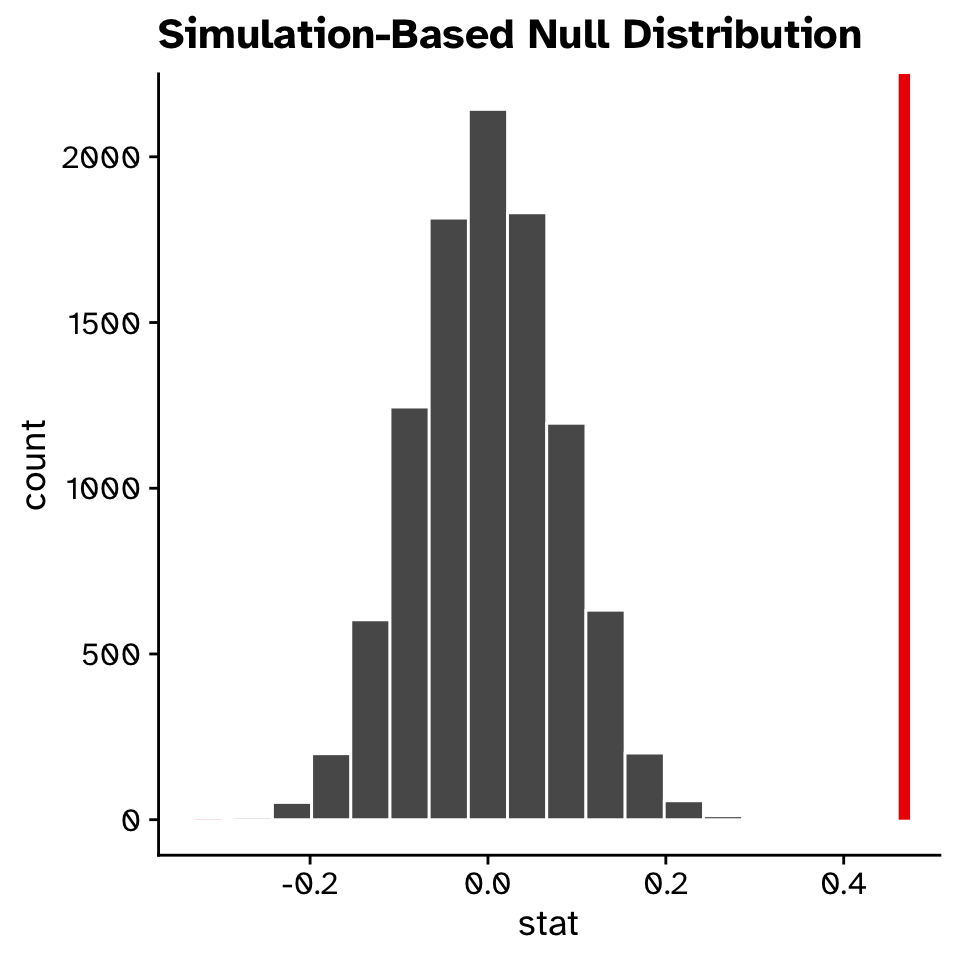
  calculate(stat = "correlation")

Correlation

Hypothesis test

visualize(null_dist) +
  shade_p_value(obs_stat = observed_correlation, direction = "two-sided")

Correlation

Hypothesis test

null_dist |>
  get_p_value(obs_stat = observed_correlation, direction = "two-sided")

# A tibble: 1 × 1
  p_value
    <dbl>
1       0

Remember that our p-value is an approximation
- The number of decimal places of accuracy we can observe is directly linked to the number of reps

Regression

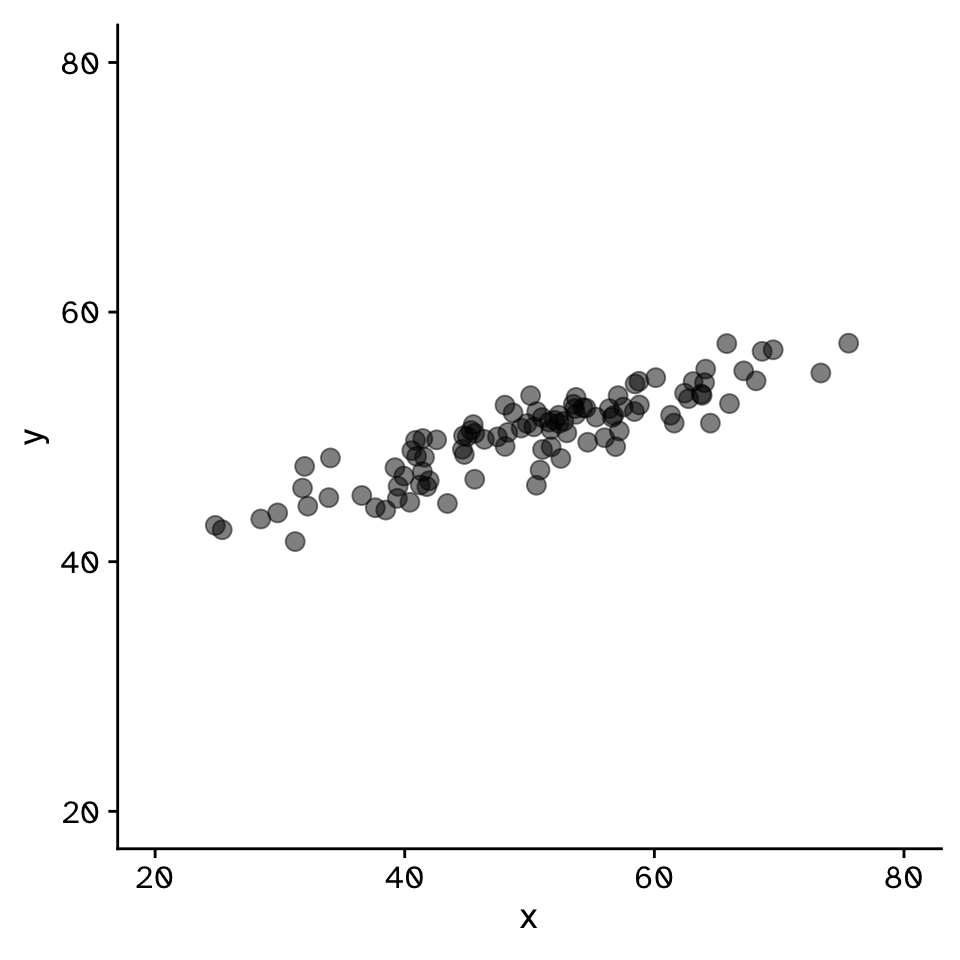
How does variable Y depend on variable X

A mathmatical function describing the relationship between two continuous variables
Y is dependant on X (the)
Y is a function of X
Predictive model
Very powerful framework

Regression

How does variable Y depend on variable X

\[ y = \text{Slope}\times x + \text{Intercept} \]

\[ y = mx+c \]

\[ y = \beta_1x+\beta_0 \]

\[ y = \beta_0+\beta_1x+\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5 \]

Regression

How does variable Y depend on variable X

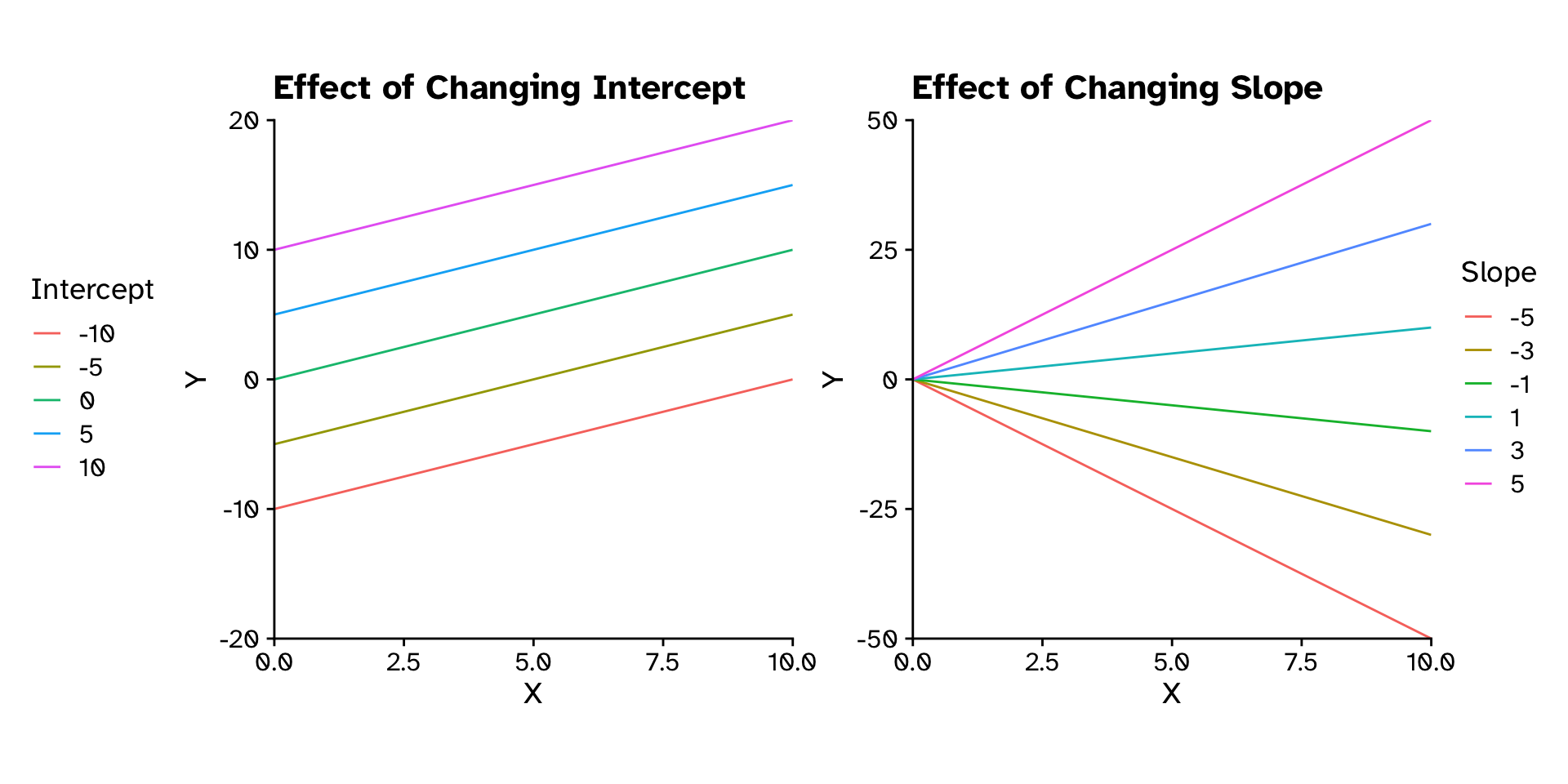
Regression

How does variable Y depend on variable X

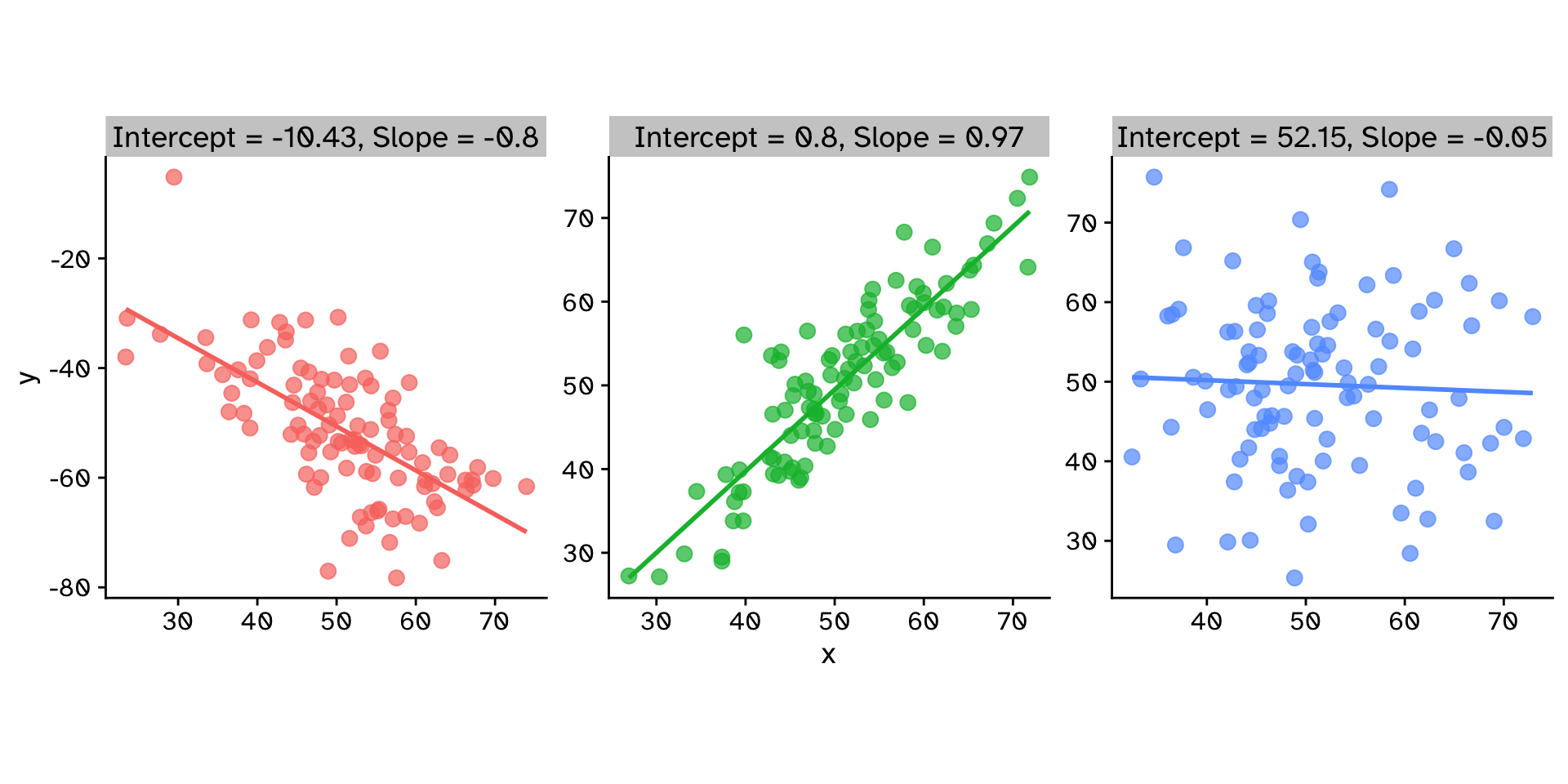
Regression

How does variable Y depend on variable X

Example: For sexual selection to operate, an increase in mating success (number of mates) must result in an increase in reproductive success (number of offspring).

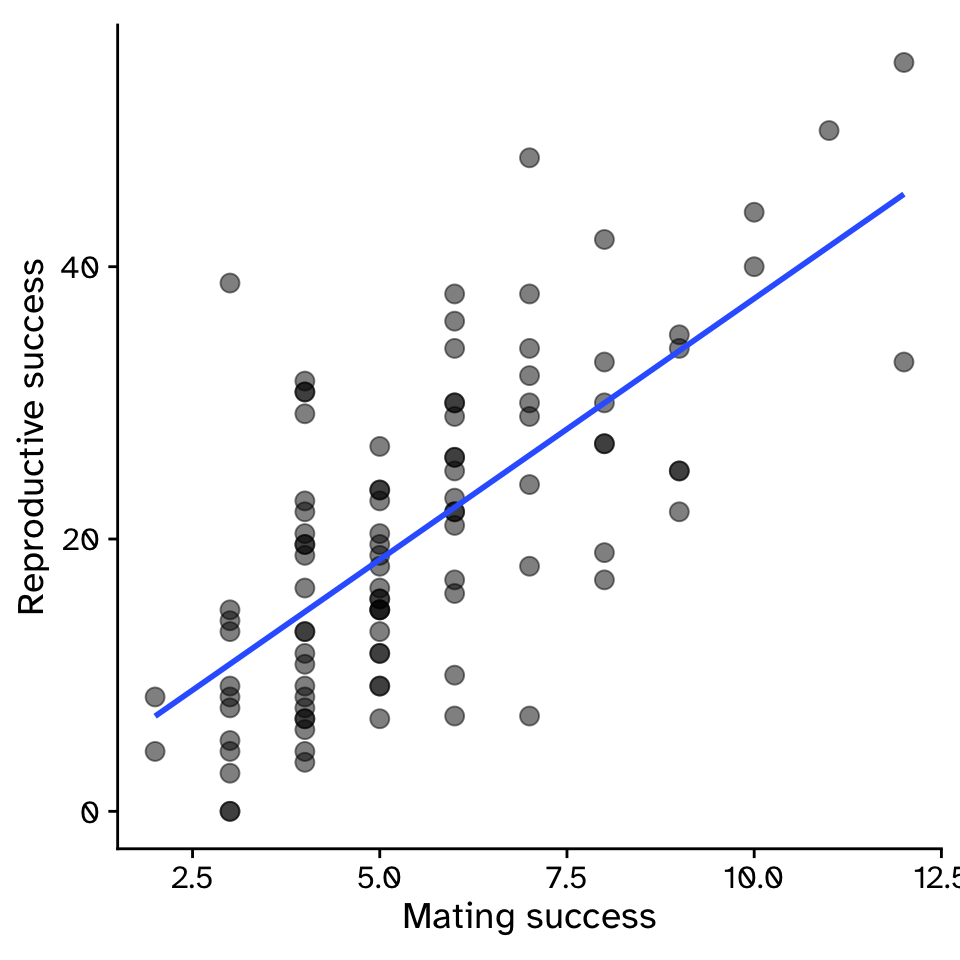
Regression

How does variable Y depend on variable X

\[ y = \beta_1x+\beta_0 \]

\[ y = 3.83x-0.68 \]

\(\beta_1\) = strength of sexual selection
For each additional mate, an individual (on average) gains \(\beta_1\) additional offspring
For 5 mates (\(x=5\)):
- \(y = 3.83\times5-0.68\)
- \(y = 18.47\)

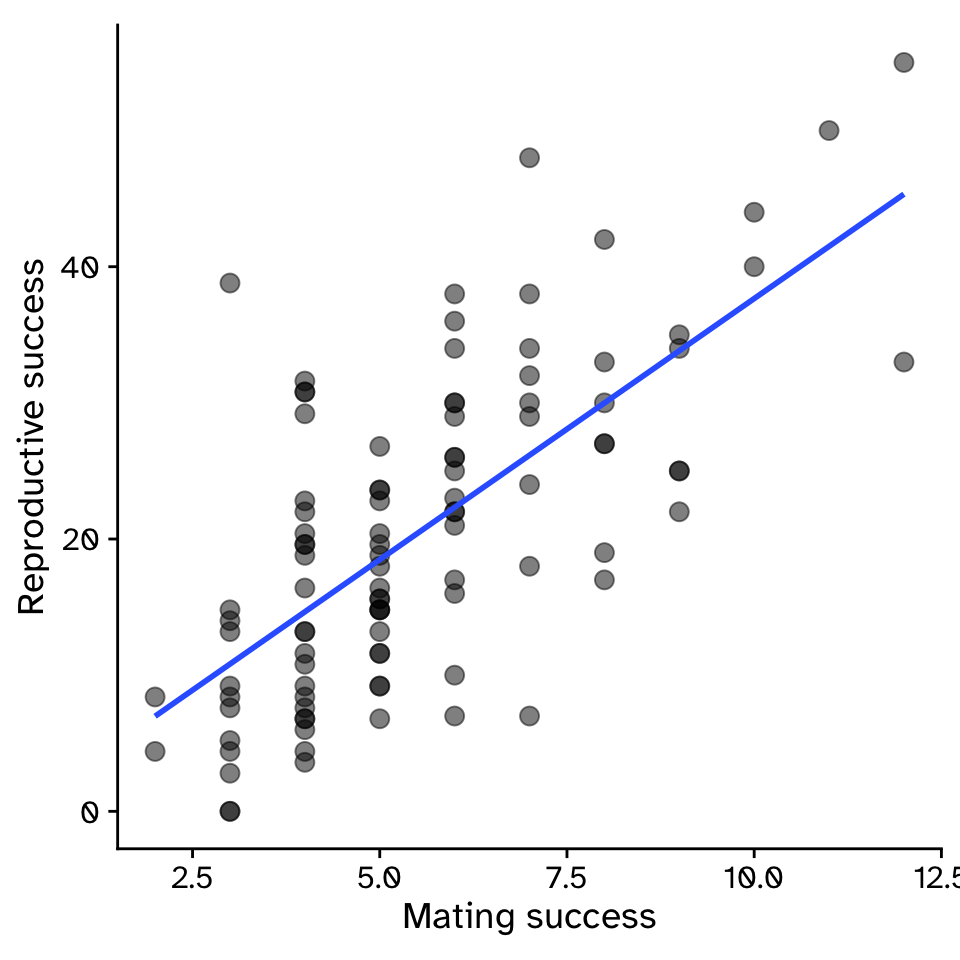
Regression

How does variable Y depend on variable X

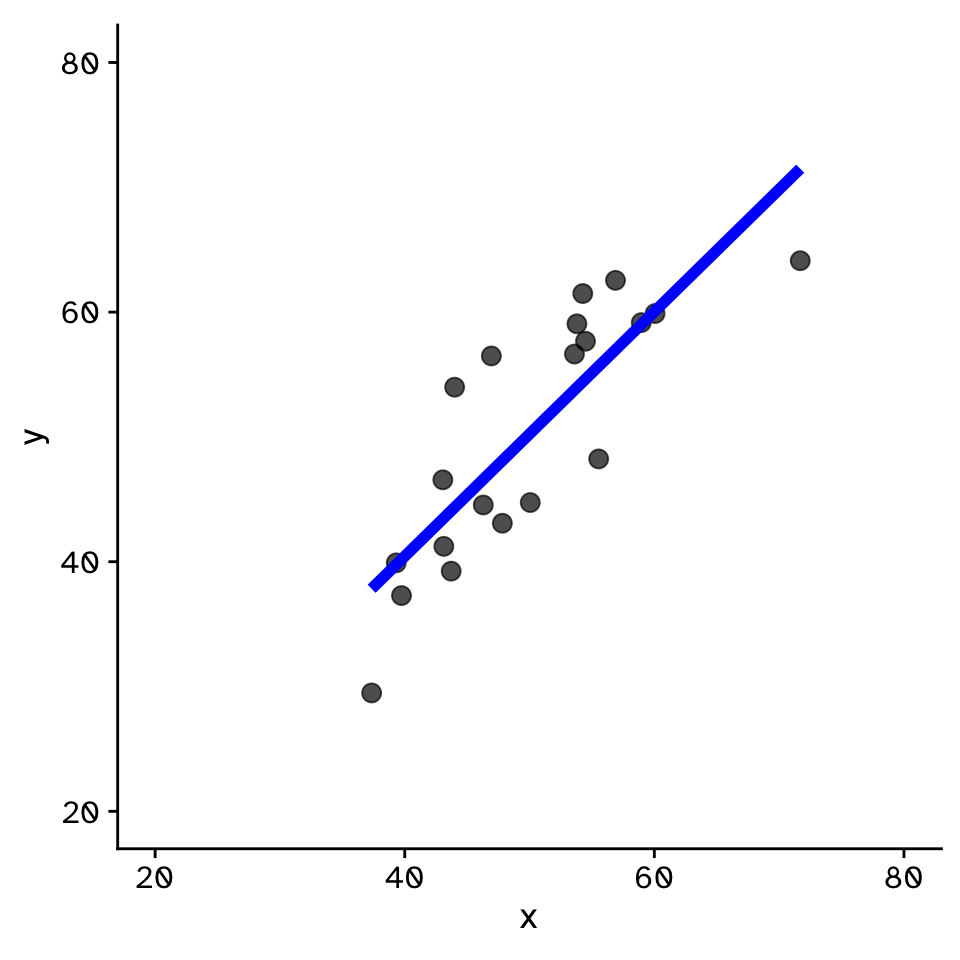
Regression

How does variable Y depend on variable X

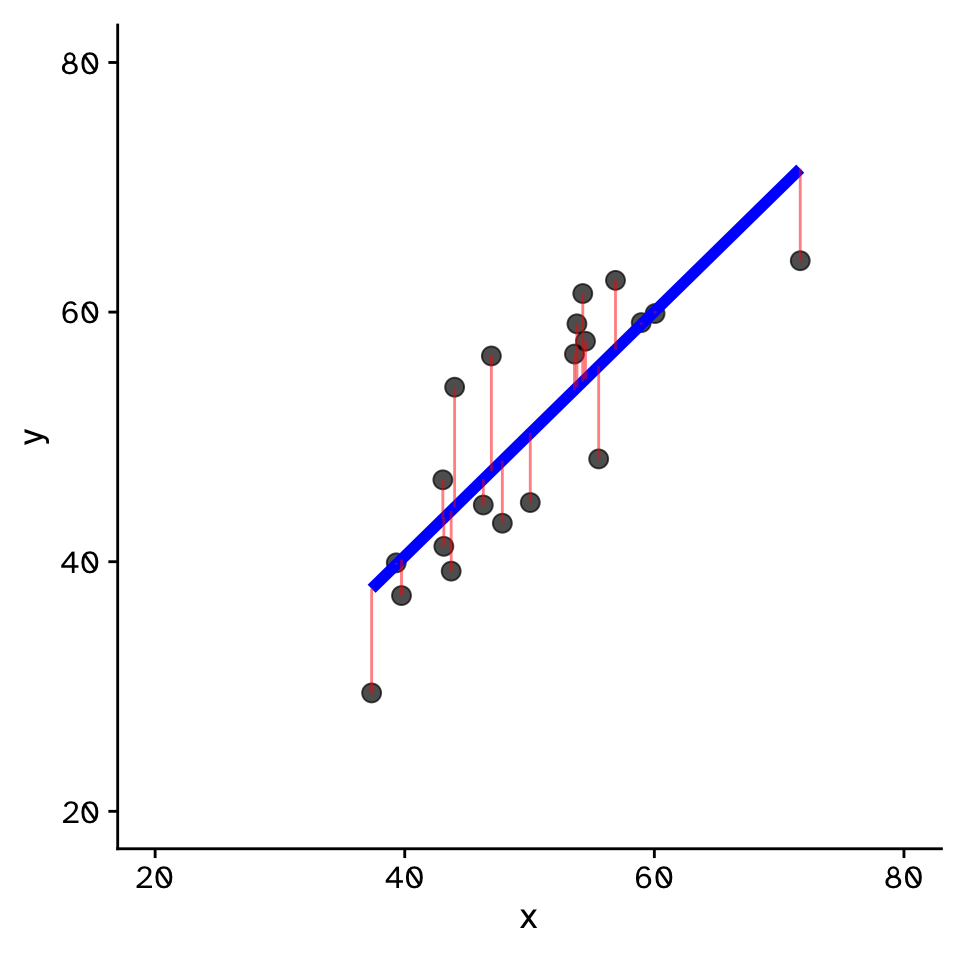
Regression

How does variable Y depend on variable X

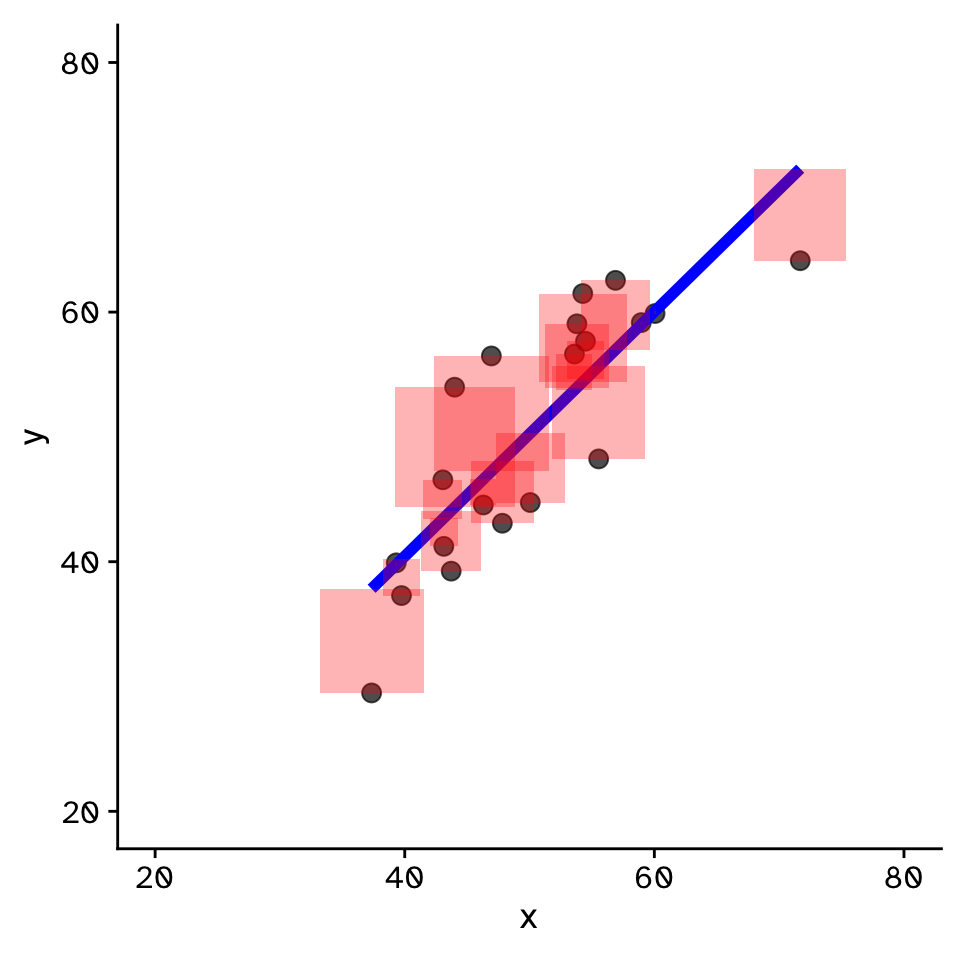
Regression

How does variable Y depend on variable X

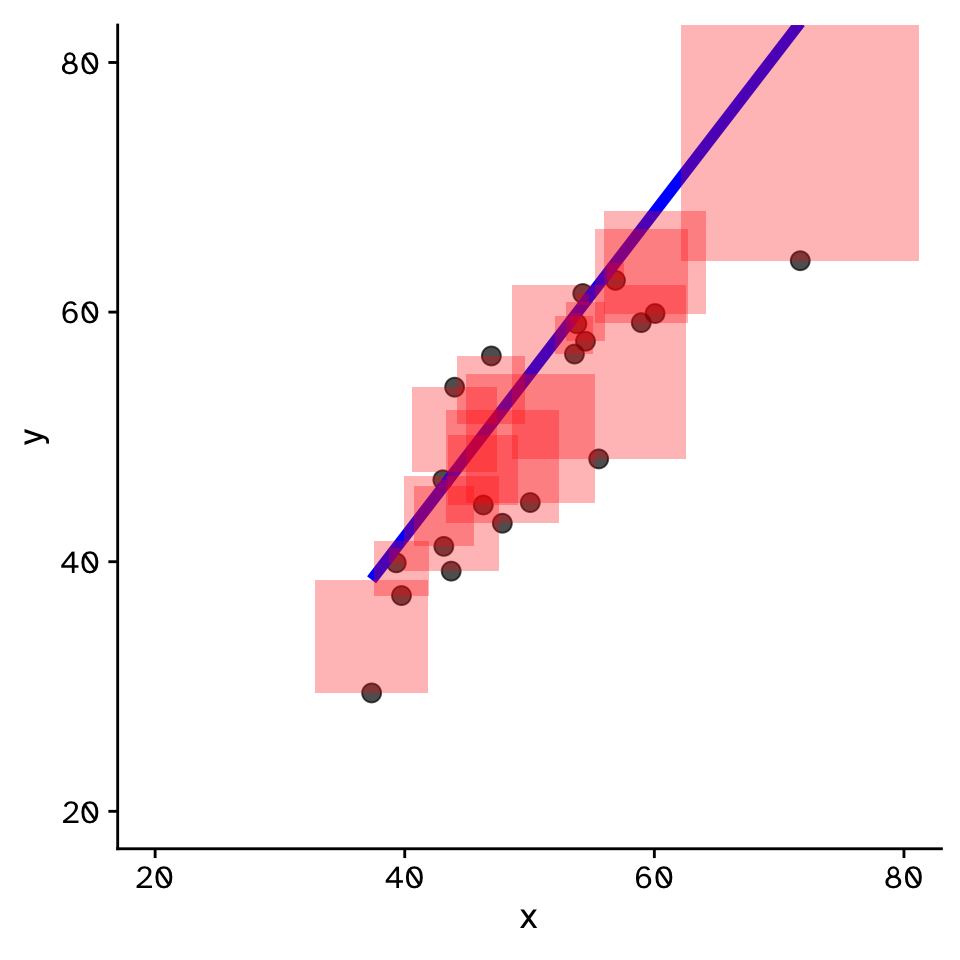
Regression

How does variable Y depend on variable X

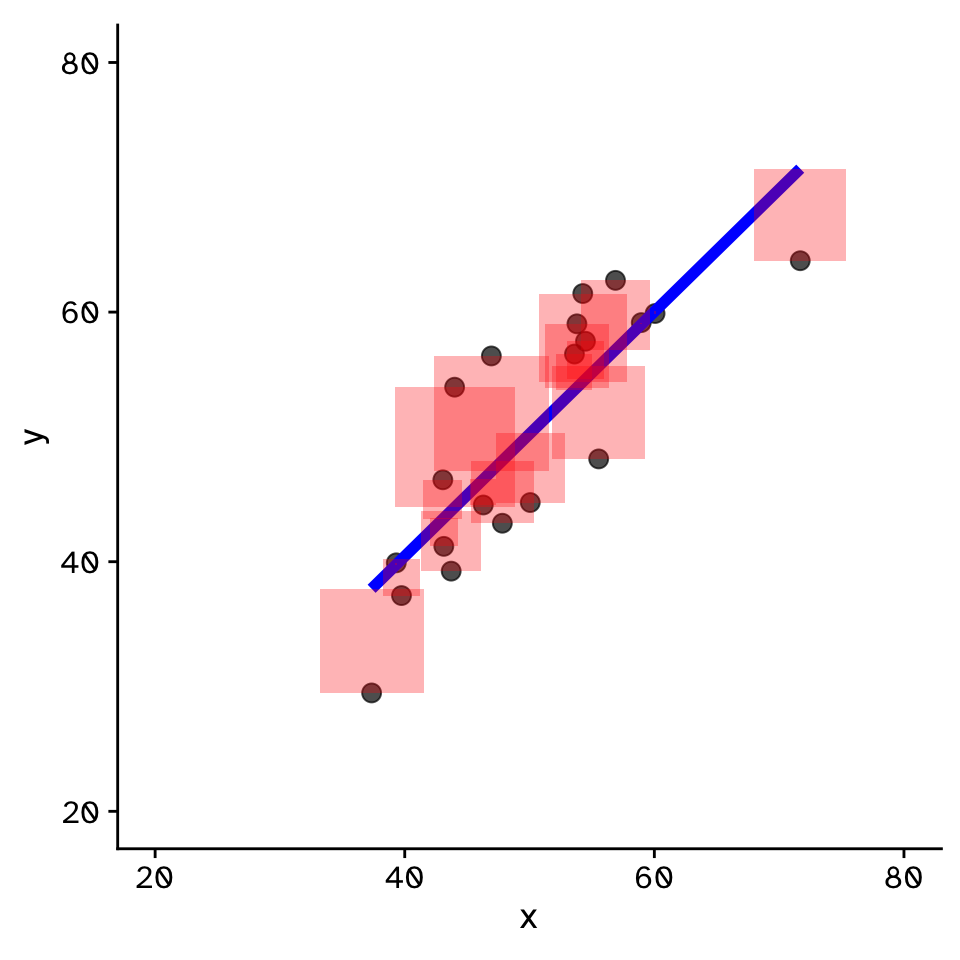
Fit by solving to minimise the sum of the squared residuals (SSR)
- Find \(\beta_1\) and \(\beta_0\) that minimise the SSR
- Called a “loss function”
- Many approaches to do this!

Regression

How does variable Y depend on variable X

Regression

How to fit in R?

Base R:

lm(data = mating_data, reproductive_success ~ mating_success)


Call:
lm(formula = reproductive_success ~ mating_success, data = mating_data)

Coefficients:
   (Intercept)  mating_success  
       -0.6844          3.8344

Regression

How to fit in R?

With infer:

observed_fit <-
  mating_data |>
  specify(reproductive_success ~ mating_success) |>
  fit()

observed_fit

# A tibble: 2 × 2
  term           estimate
  <chr>             <dbl>
1 intercept        -0.684
2 mating_success    3.83

Regression

Confidence intervals

boot_dist <-
  mating_data |>
  specify(reproductive_success ~ mating_success) |>
  generate(reps = 1000, type = "bootstrap") |>
  fit()

boot_dist

# A tibble: 2,000 × 3
# Groups:   replicate [1,000]
   replicate term           estimate
       <int> <chr>             <dbl>
 1         1 intercept        -3.75 
 2         1 mating_success    4.32 
 3         2 intercept        -4.96 
 4         2 mating_success    4.73 
 5         3 intercept        -0.267
 6         3 mating_success    3.80 
 7         4 intercept         6.72 
 8         4 mating_success    2.84 
 9         5 intercept        -1.08 
10         5 mating_success    3.96 
# ℹ 1,990 more rows

Regression

Confidence intervals

conf_ints <- 
  get_confidence_interval(
    boot_dist, 
    level = .95, 
    point_estimate = observed_fit
  )

conf_ints

# A tibble: 2 × 3
  term           lower_ci upper_ci
  <chr>             <dbl>    <dbl>
1 intercept         -5.33     4.36
2 mating_success     2.99     4.66

Regression

Confidence intervals

visualize(boot_dist) +
  shade_confidence_interval(endpoints = conf_ints)

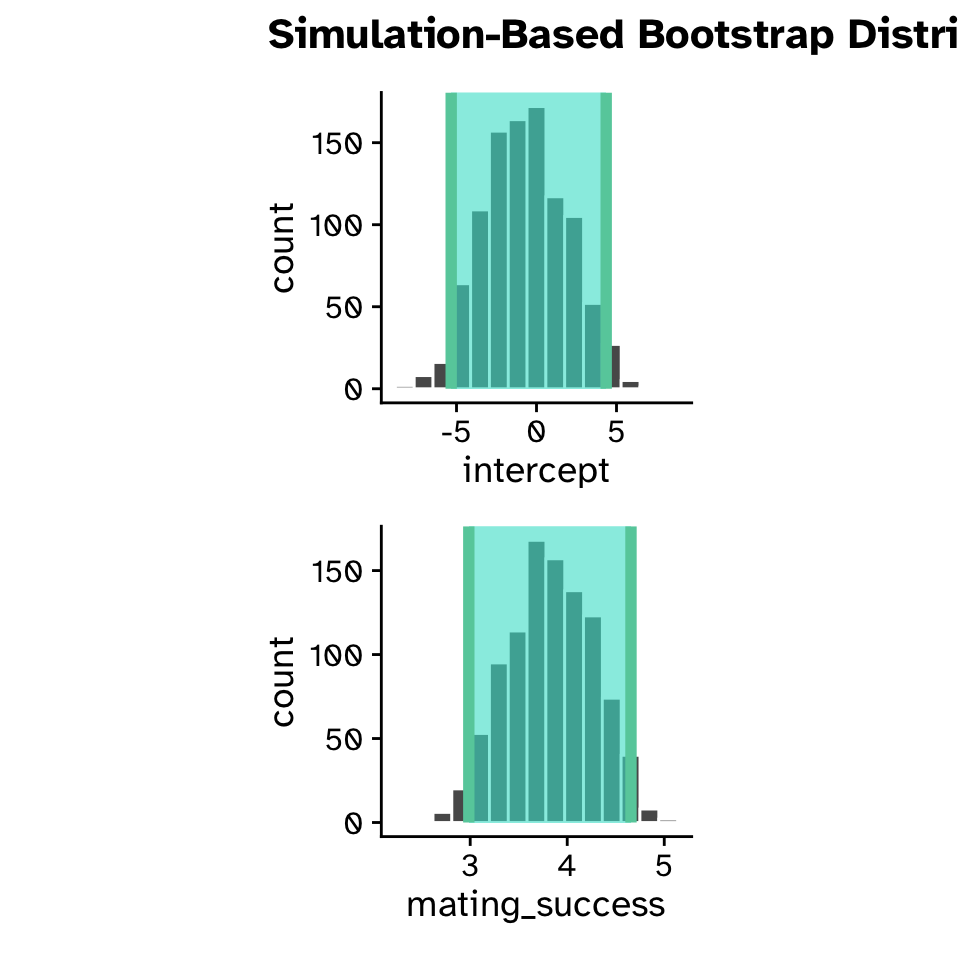
Regression

Hypothesis test

Null hypothesis:
- Slope = 0
Alternative hypothesis:
- Slope \(\neq\) 0
- Slope < 0
- Slope > 0

Regression

Hypothesis test

null_dist <-
  mating_data |>
  specify(reproductive_success ~ mating_success) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  fit()

null_dist

# A tibble: 2,000 × 3
# Groups:   replicate [1,000]
   replicate term           estimate
       <int> <chr>             <dbl>
 1         1 intercept       20.3   
 2         1 mating_success   0.0382
 3         2 intercept       23.9   
 4         2 mating_success  -0.603 
 5         3 intercept       25.8   
 6         3 mating_success  -0.951 
 7         4 intercept       23.7   
 8         4 mating_success  -0.570 
 9         5 intercept       27.2   
10         5 mating_success  -1.20  
# ℹ 1,990 more rows

Regression

Hypothesis test

visualize(null_dist) +
  shade_p_value(obs_stat = observed_fit, direction = "two-sided")

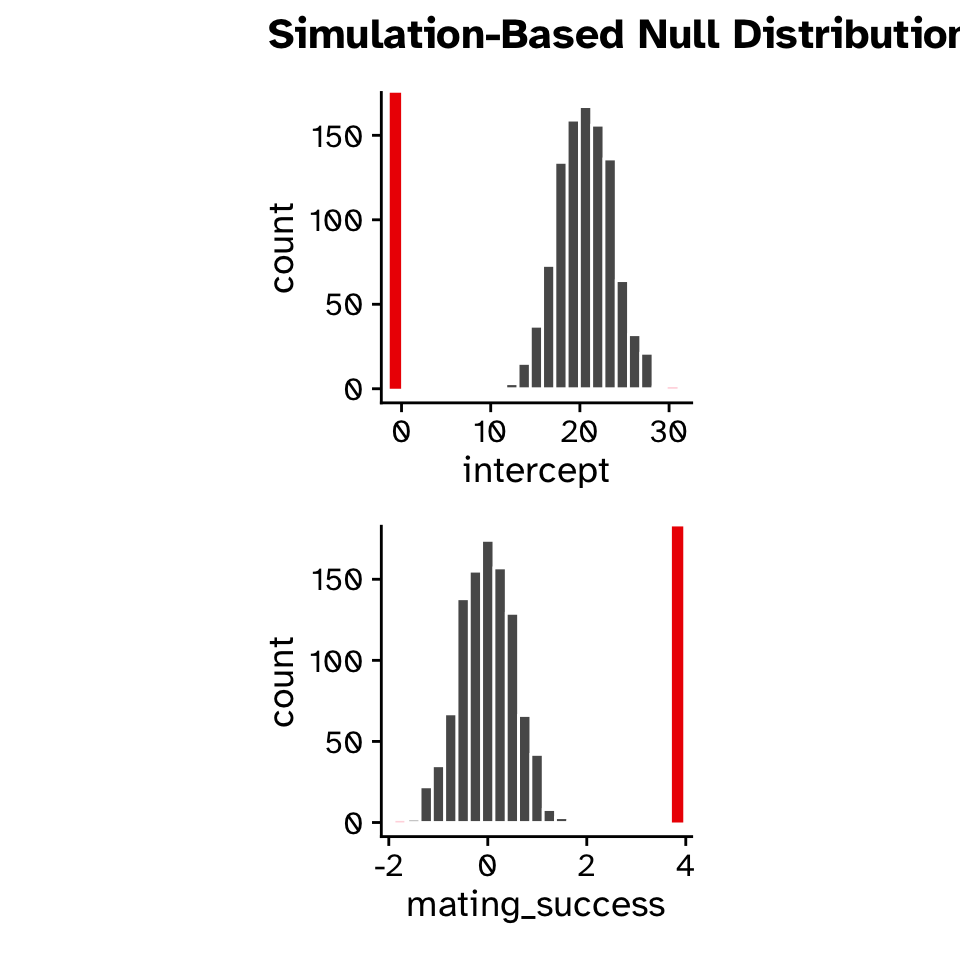
Regression

Hypothesis test

null_dist |>
  get_p_value(obs_stat = observed_fit, direction = "two-sided")

# A tibble: 2 × 2
  term           p_value
  <chr>            <dbl>
1 intercept            0
2 mating_success       0

Regression

Multiple regression

\[ y = \beta_1x+\beta_0 \]

\[ y = \beta_0+\beta_1x+\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5 \]

data |>
specify(reproductive_success ~ mating_success + sex + feather_colour) ...

Sokal, R. R., and F. J. Rohlf. 1995. Biometry. https://lubcat.lub.lu.se/cgi-bin/koha/opac-detail.pl?biblionumber=2483009.