Computational statistics
Lecture 2
BIOC13 - Ekologi
Department of Biology, Lund University
2025-04-25
Review
Review
Populations and Samples
Review
Populations and Samples
| region | host_plant | patry | sex | body_length_mm | ovipositor_length_mm | wing_length_mm | wing_width_mm | melanized_percent | baltic |
|---|---|---|---|---|---|---|---|---|---|
| estonia | heterophyllum | sympatry | male | 3.94 | NA | 4.455026 | 1.873016 | 55.96312 | east |
| estonia | heterophyllum | sympatry | female | 4.48 | 1.65 | 4.710000 | 2.170000 | 63.89701 | east |
| estonia | heterophyllum | sympatry | male | 4.61 | NA | 4.990196 | 2.294118 | 62.52199 | east |
| estonia | heterophyllum | sympatry | female | 5.31 | 1.78 | 5.611650 | 2.582524 | 61.37781 | east |
| estonia | heterophyllum | sympatry | male | 4.51 | NA | 4.468750 | 2.093750 | 62.25657 | east |
| estonia | heterophyllum | sympatry | male | 4.74 | NA | 4.906250 | 2.333333 | 57.46406 | east |
Review
Populations and Samples
Review
Populations and Samples
Review
Populations and Samples
Review
Populations and Samples
Review
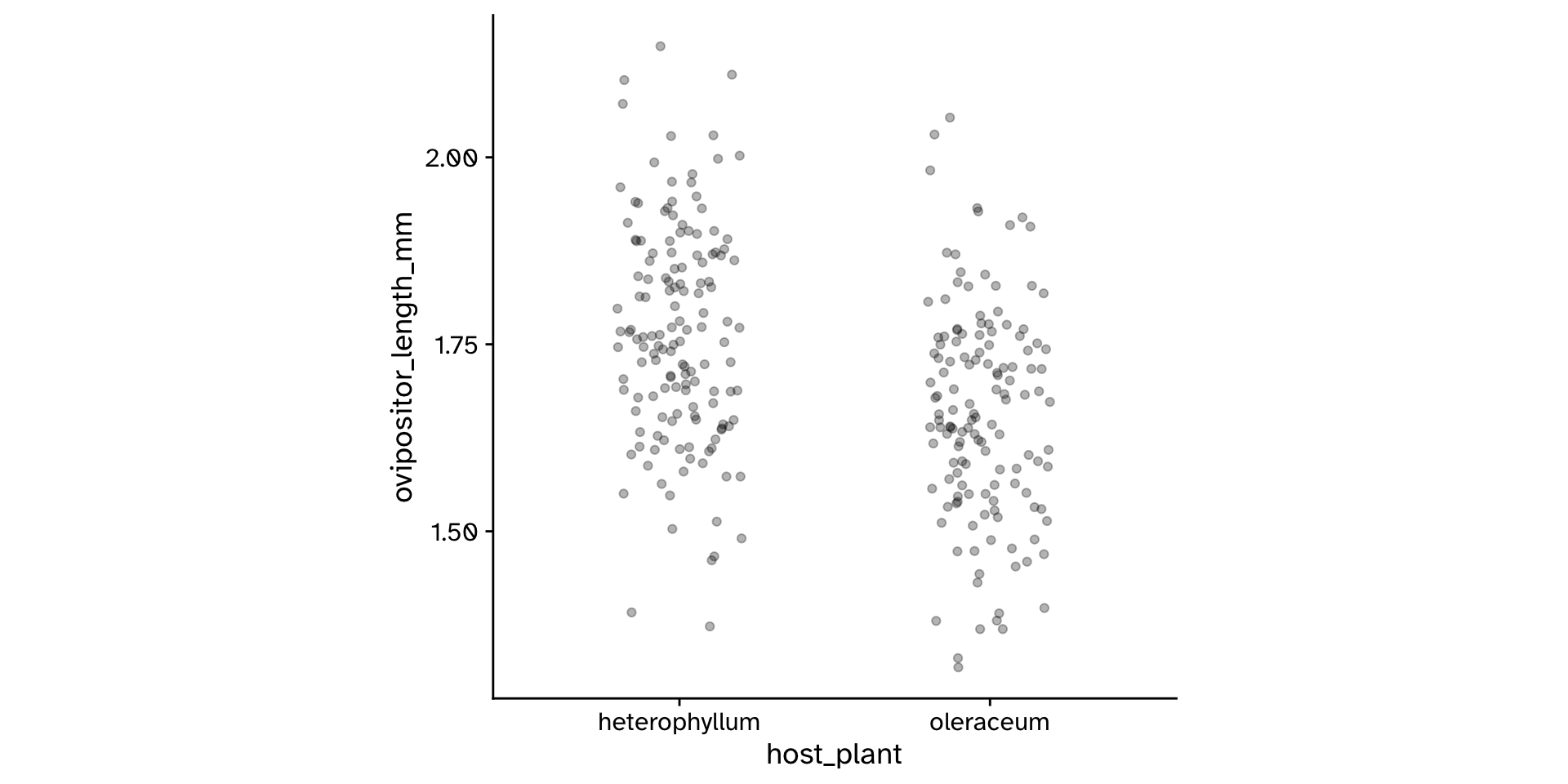
Research question
- Do flies that use
"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plantdiffer in theirovipositor_length_mm?
Review
Observed statistic
obs_stat <-
tephritis_data |>
specify(response = ovipositor_length_mm, explanatory = host_plant) |>
calculate(stat = "diff in means", order = c("heterophyllum", "oleraceum"))
obs_statResponse: ovipositor_length_mm (numeric)
Explanatory: host_plant (factor)
# A tibble: 1 × 1
stat
<dbl>
1 0.108- Was this just luck? What would happen if I measured another 600 flies?
Review
The sampling distribution
Review
The sampling distribution
- Problem: we (usually) only collect one sample
Review
The sampling distribution
- Problem: we (usually) only collect one sample
- One (of many) solutions: resample our sample (with replacement) to generate more samples
- Bootstrap resampling
- Assumes that our sample is representative of the population!
Review
The bootstrap sampling distibution
Review
The bootstrap sampling distibution
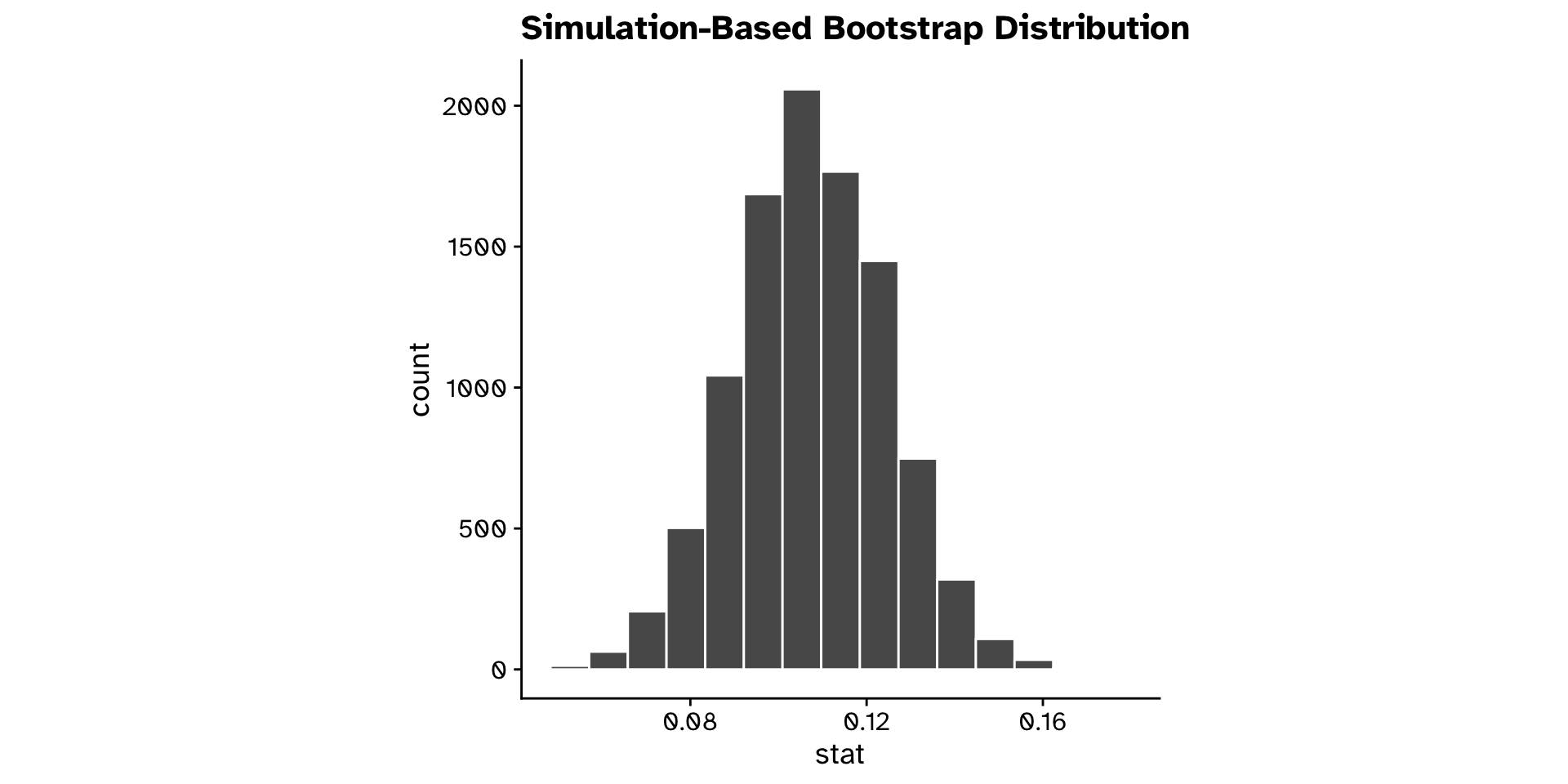
Example in R for a difference in means:
library(infer)
boot_dist <-
1 tephritis_data |>
2 specify(response = ovipositor_length_mm, explanatory = host_plant) |>
3 generate(reps = 10000, type = "bootstrap") |>
4 calculate(stat = "diff in means", order = c("heterophyllum", "oleraceum"))- 1
- Name of the dataset we are working with.
- 2
-
specifywhich variables we are interested in. - 3
-
generatenew samples with bootstrap resampling. - 4
-
calculatethe chosen statistic for each new sample generated.
Review
The bootstrap sampling distibution
Review
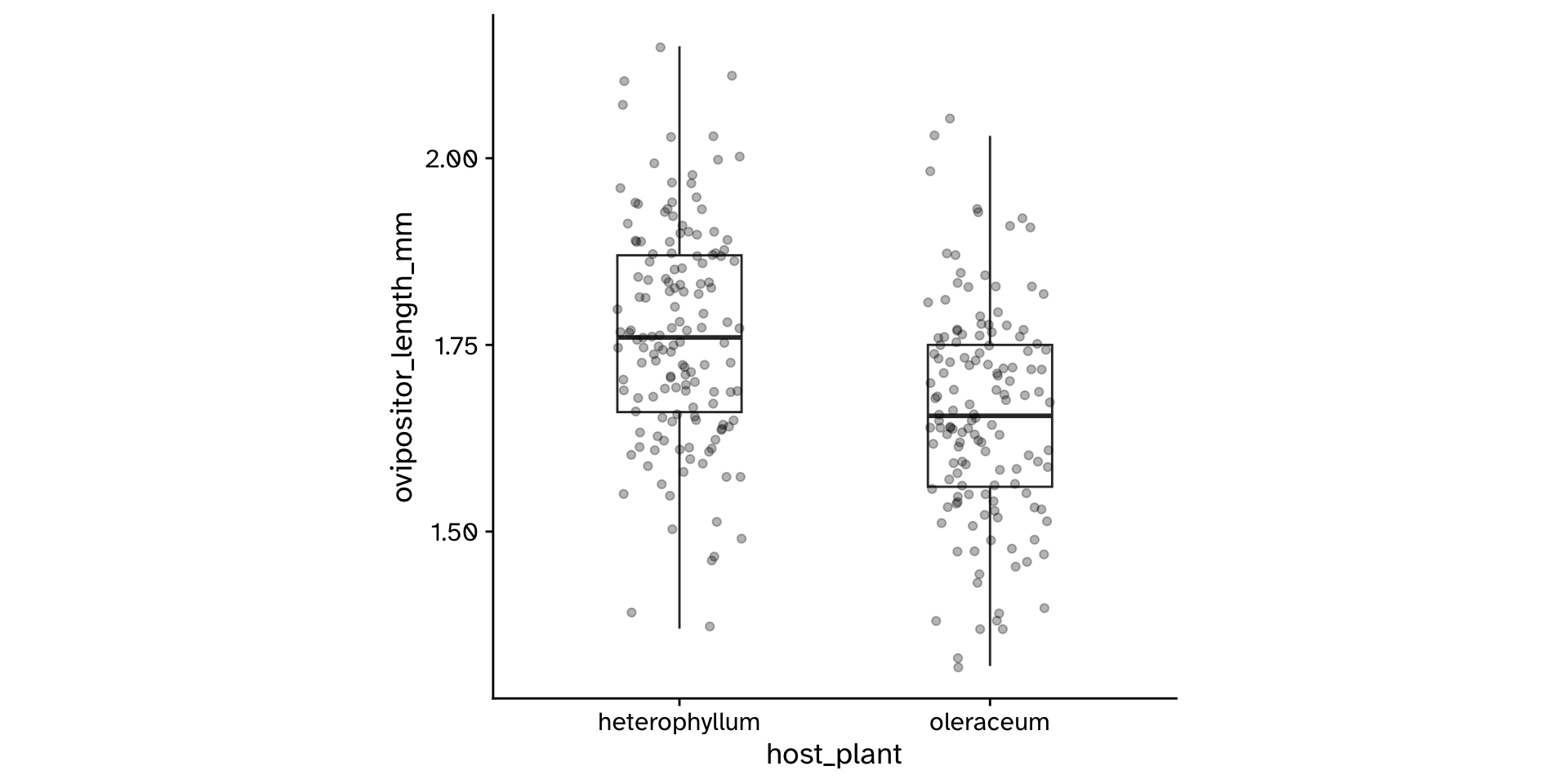
Research question
- Do flies that use
"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plantdiffer in theirovipositor_length_mm?
Response: ovipositor_length_mm (numeric)
Explanatory: host_plant (factor)
# A tibble: 1 × 1
stat
<dbl>
1 0.108- What would happen if we sampled again?
Review
Confidence intervals
Review
Confidence intervals
- If we collected another sample of the same size, how much would our test statistic be likely to vary?
- Percentile method
- middle X% of sampling distribution
Review
Confidence intervals
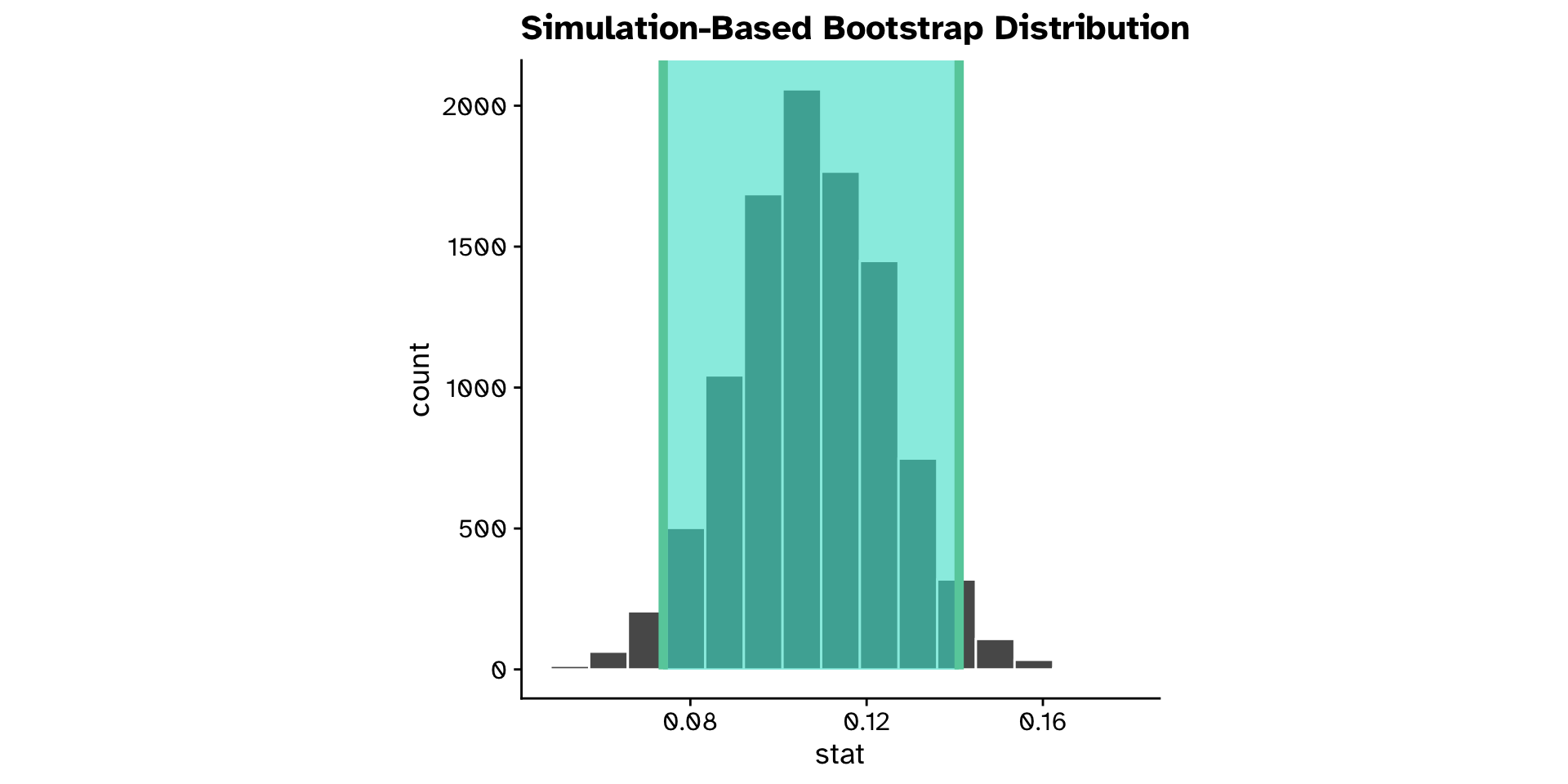
Example in R:
- 1
- The bootstrap sampling distribution
- 2
-
Function from
inferto calculate a 95% CI with"percentile"method
Review
Confidence intervals
Review
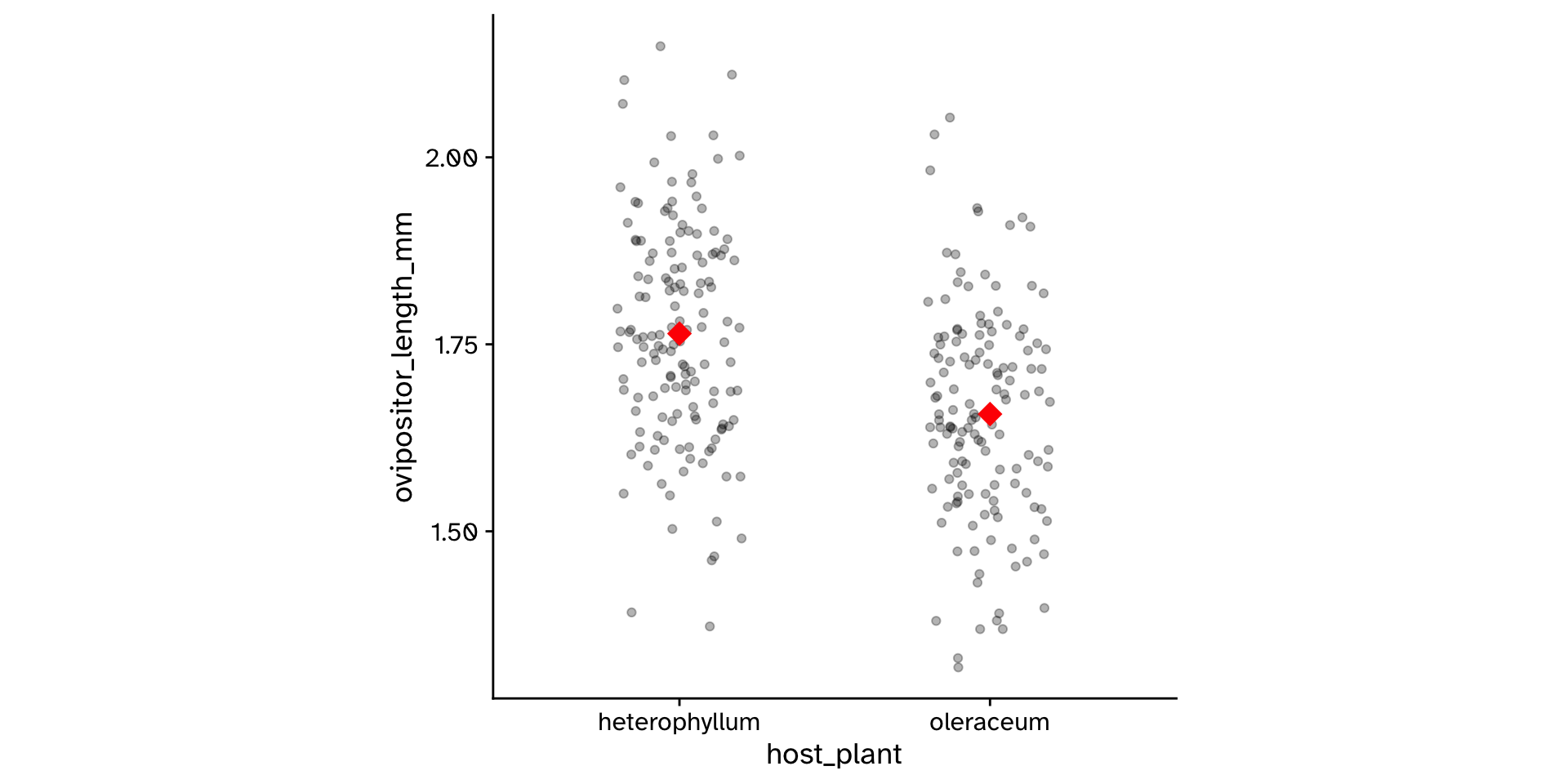
Research question
- Do flies that use
"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plantdiffer in theirovipositor_length_mm?
Response: ovipositor_length_mm (numeric)
Explanatory: host_plant (factor)
# A tibble: 1 × 1
stat
<dbl>
1 0.108- What would happen if we sampled again?
- We are pretty sure the difference would be between:
Review
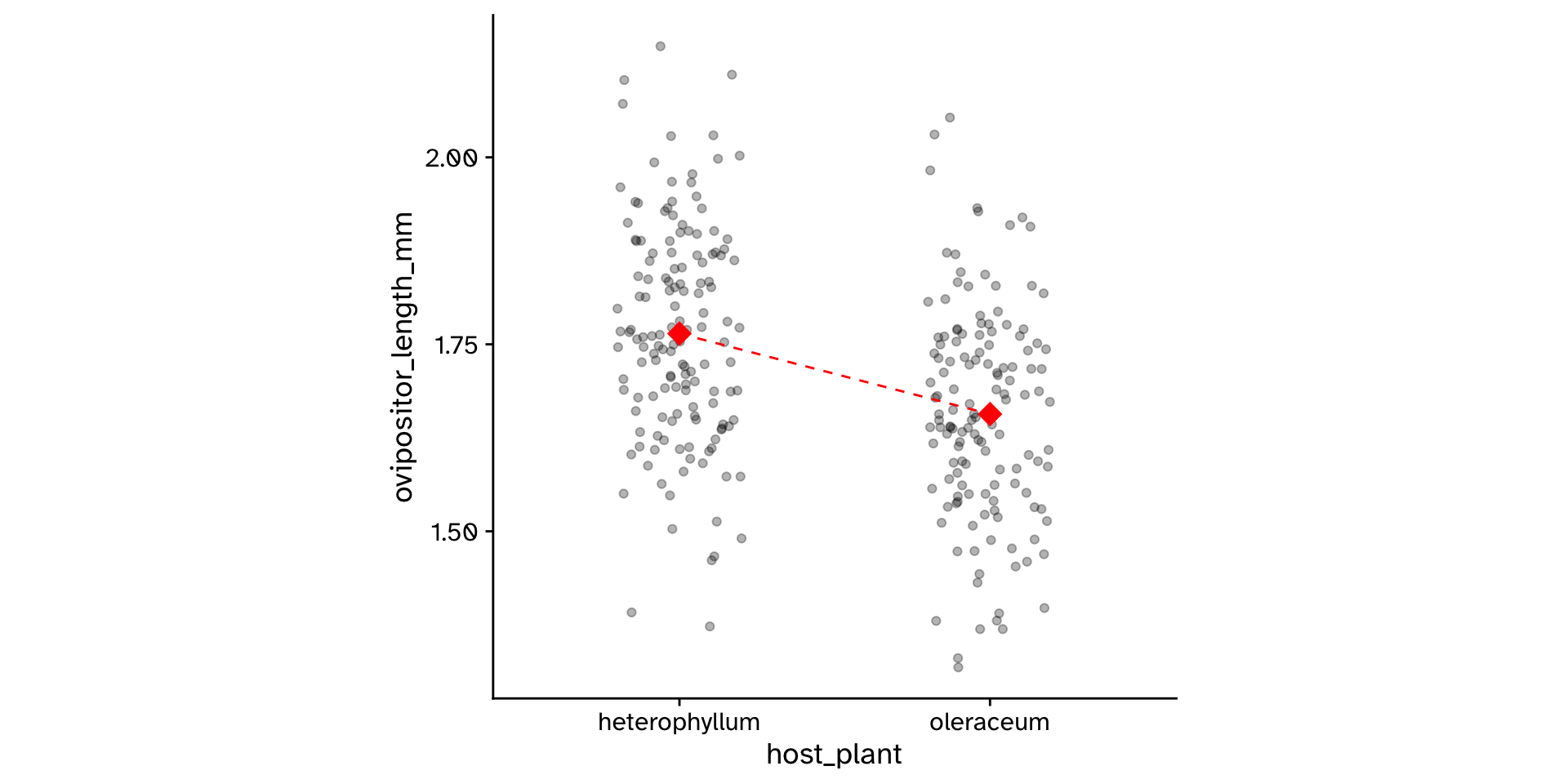
Research question
- Do flies that use
"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plantdiffer in theirovipositor_length_mm?- Observed difference in means: 0.108
- 95% confidence interval: 0.074 - 0.141
Review
Research question
- Do flies that use
"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plantdiffer in theirovipositor_length_mm?- Observed difference in means: 0.108
- 95% confidence interval: 0.074 - 0.141
- Could we have observed this if there was truly no difference?
Review
Hypothesis testing
Review
Hypothesis testing
- Null hypothesis
- There is no difference in
ovipositor_length_mmbetween flies that use"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plant.
- There is no difference in
- Alternative hypothesis
- There is difference in
ovipositor_length_mmbetween flies that use"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plant.
- There is difference in
Review
Hypothesis testing
- Null hypothesis
- There is no difference in
ovipositor_length_mmbetween flies that use"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plant.
- There is no difference in
- We test to see if our sample allows us to reject the null hypothesis with sufficient confidence.
Review
Hypothesis testing
- Need to know what sort of differences we could observe if the null hypothesis was true
- Need to generate a null distribution which we will then compare our observed statistic against.
Review
Hypothesis testing
Review
Hypothesis testing
- If null hypothesis is true:
host_plantvariable has no predictive value forovipositor_length_mm- Randomly shuffling (permuting)
host_plantshould produce samples similar to observed sample
- If null hypothesis is false:
host_plantvariable has predictive value forovipositor_length_mm- Randomly shuffling (permuting)
host_plantshould produce samples different to observed sample
Review
Hypothesis testing
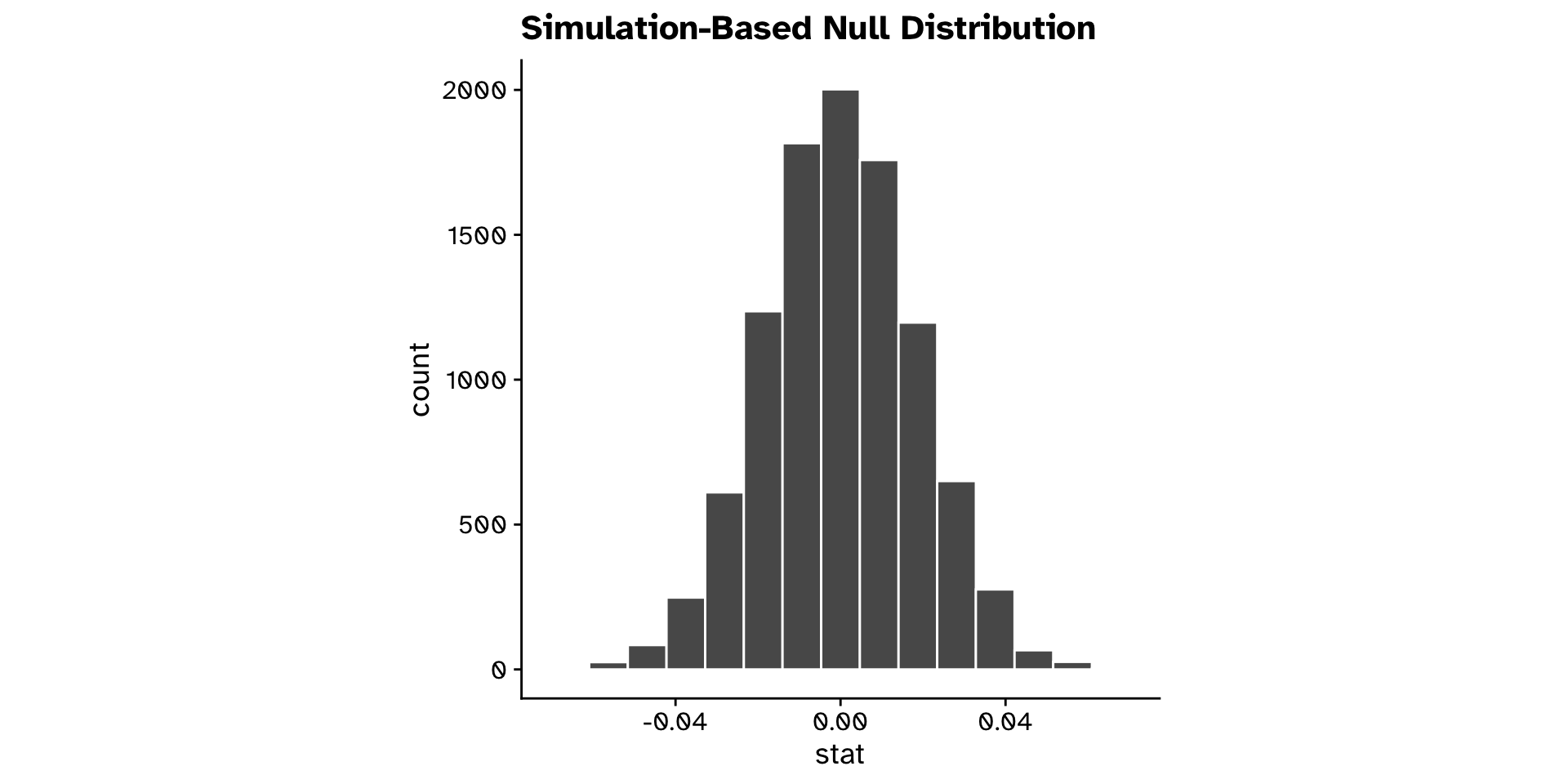
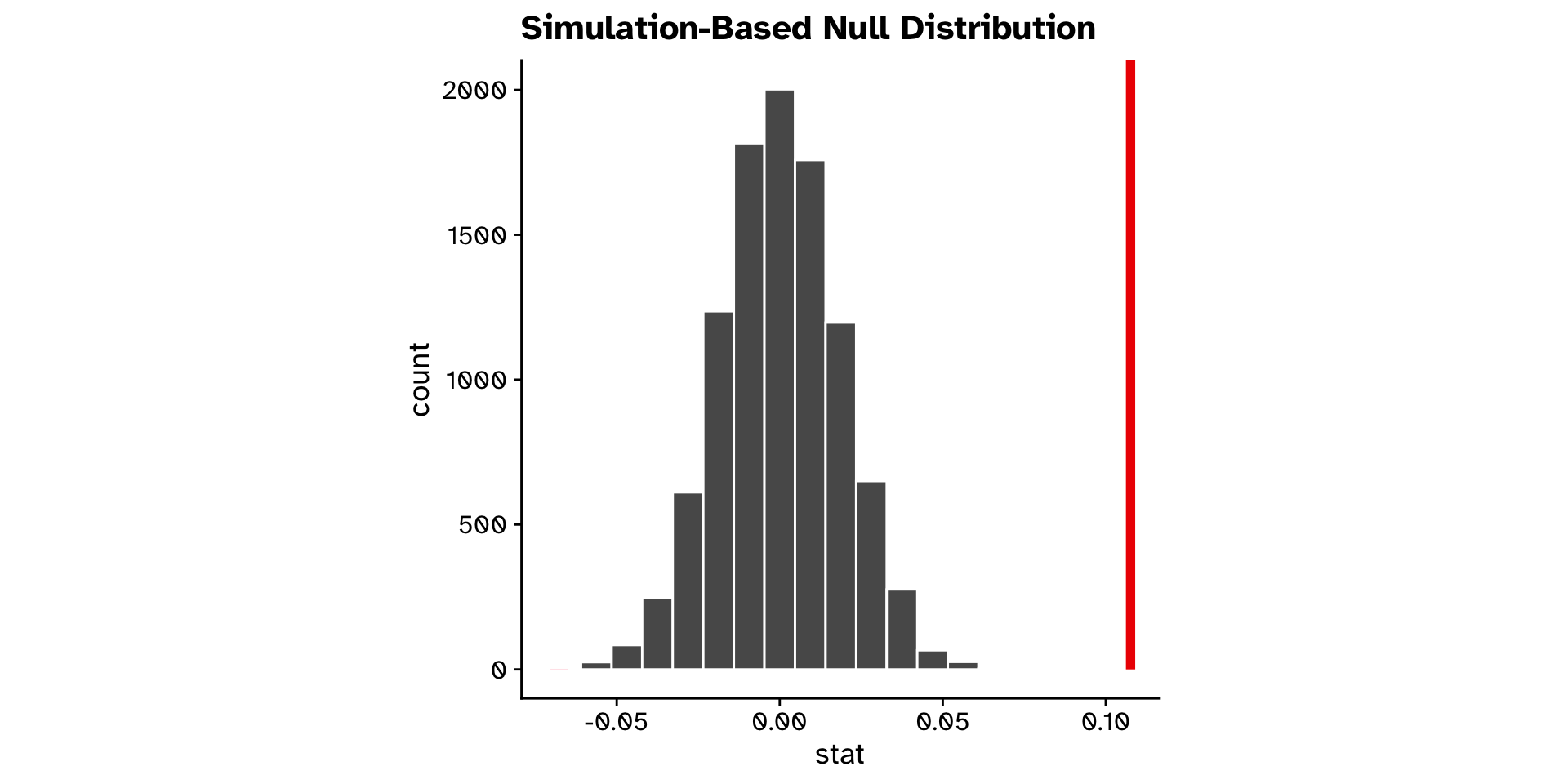
null_dist <-
tephritis_data |>
specify(response = ovipositor_length_mm, explanatory = host_plant) |>
1 hypothesise(null = "independence") |>
2 generate(reps = 10000, type = "permute") |>
calculate(stat = "diff in means", order = c("heterophyllum", "oleraceum"))- 1
-
We declare our null hypothesis to be that the
responseandexplanatoryvariables are independent of each other. - 2
- We generate 10000 permutated datasets under this hypothesis, and calculate the statistic for each dataset
Review
Hypothesis testing
Review
Hypothesis testing
Review
Hypothesis testing
Review
Research question
- Do flies that use
"heterophyllum"as ahost_plantand flies that use"oleraceum"as ahost_plantdiffer in theirovipositor_length_mm?- Observed difference in means: 0.108
- 95% confidence interval: 0.074 - 0.141
- Could we have observed this if there was truly no difference?
- Very unlikely (p < 0.0001)
How to address other research questions
Other research questions
Already covered
- Difference between two groups in a continuous variable
- Difference in means
- Can be applied to any other difference
Other research questions
Today
- Does an observed statistic differ from a hypothesised value?
- Continuous variable (mean, median, sd, etc)
- Categorical varaible (proportion)
- Difference between >2 groups in a continuous variable
- Are two (or more) distributions different?
- Is there a linear relationship between two variables?
- Do two groups differ in their relationship between two variables?
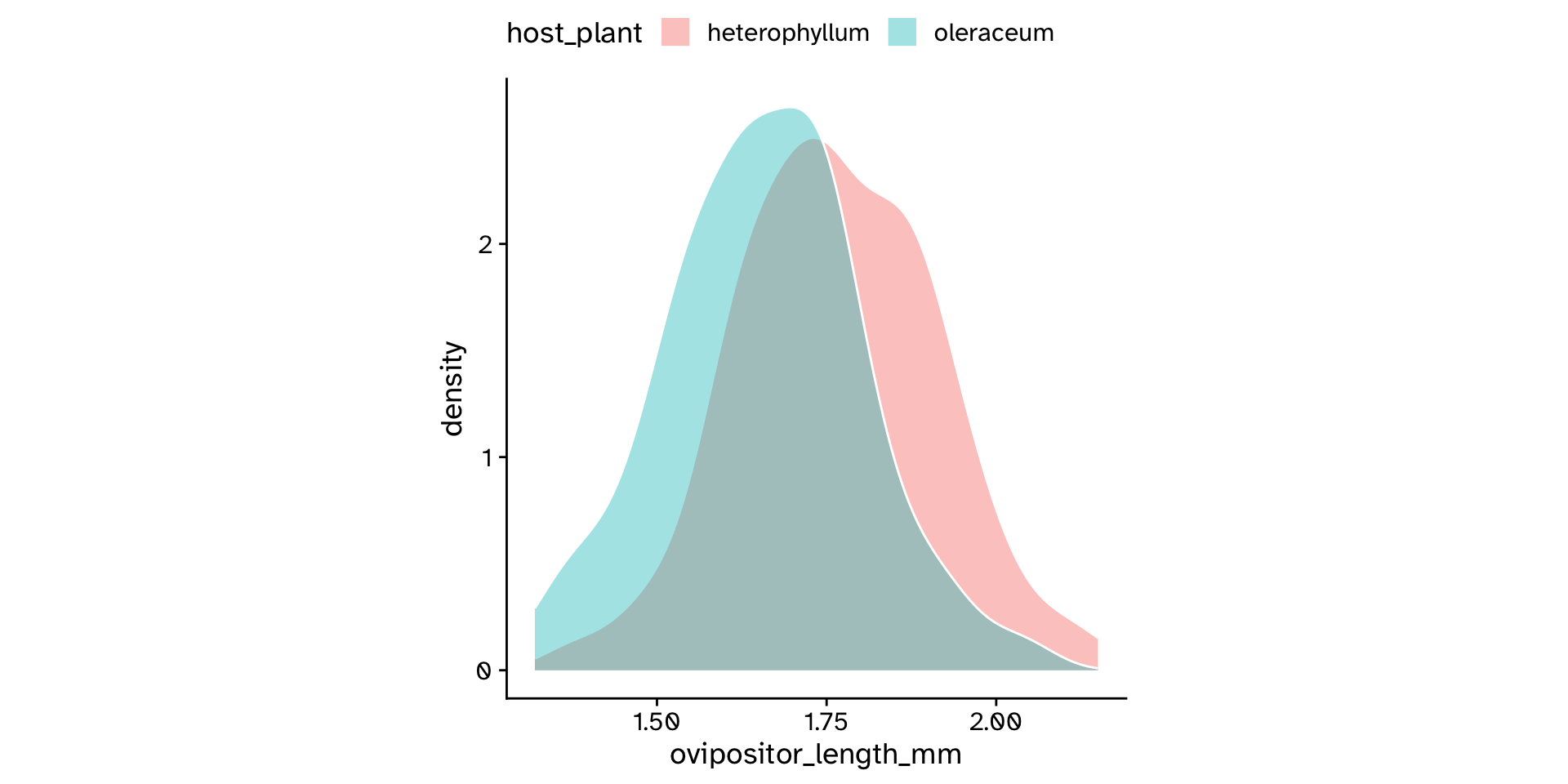
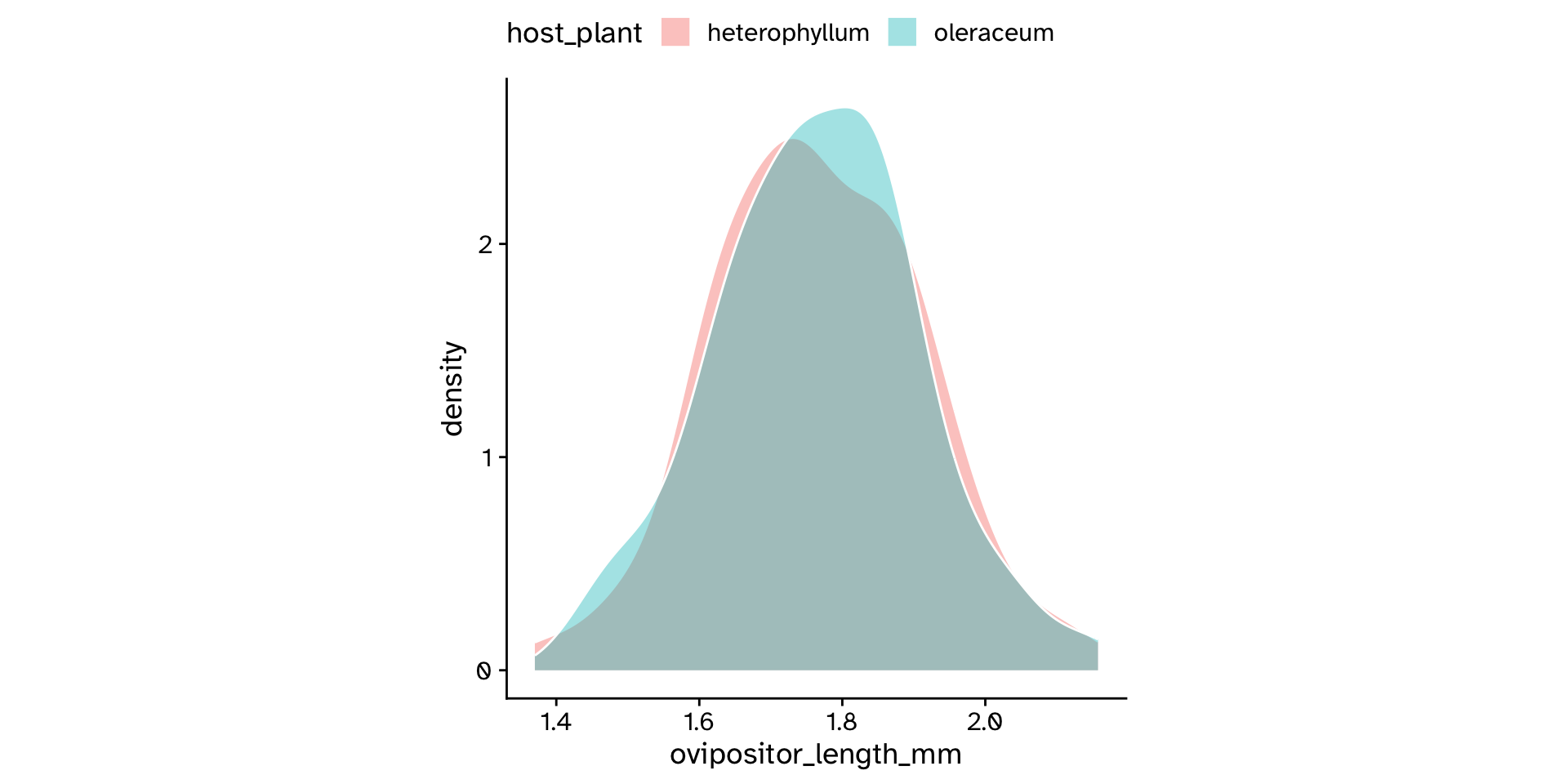
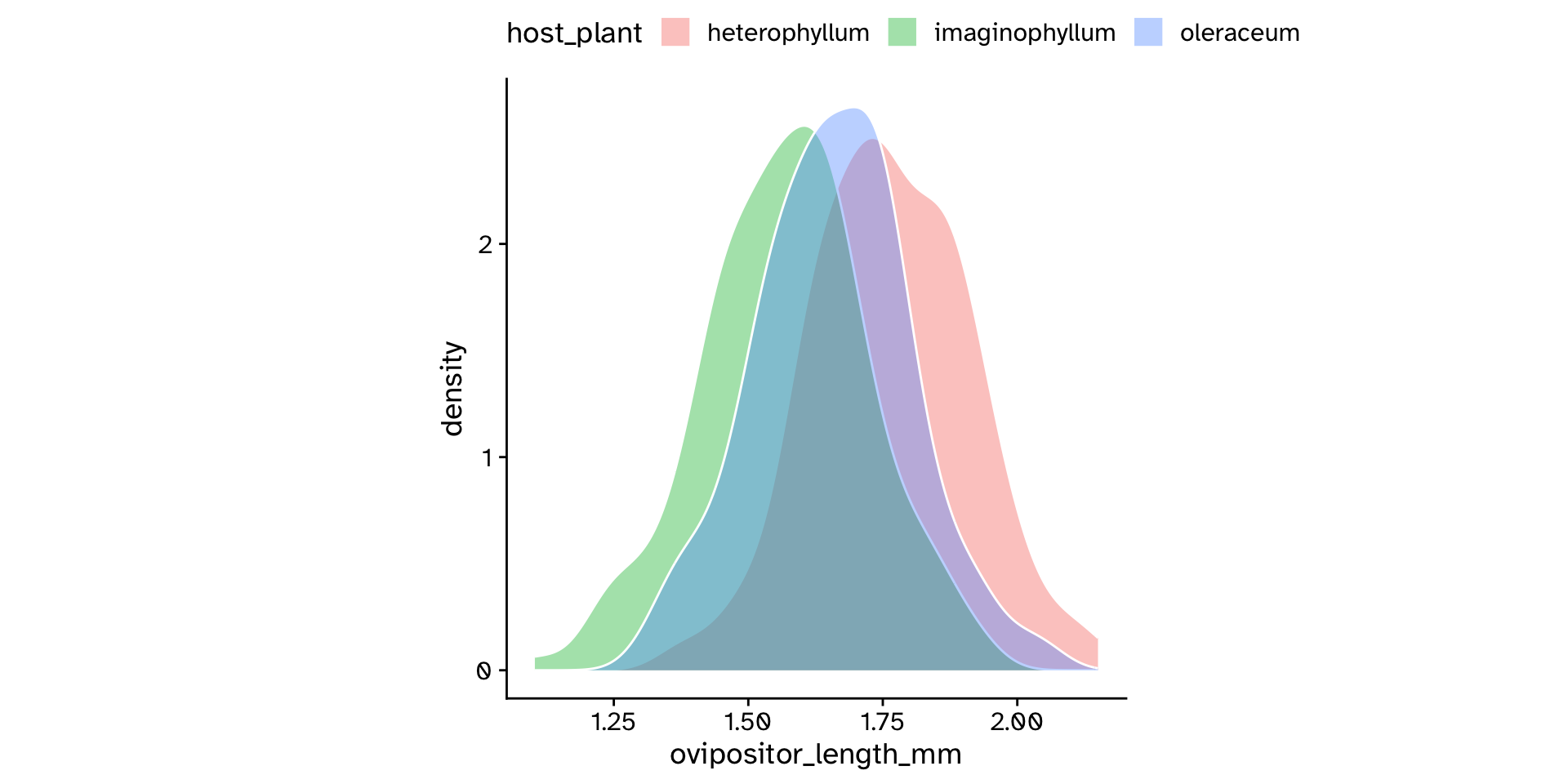
Difference between >2 groups in a continuous variable
Comparing means between >2 groups
Analysis of Variance (ANOVA)
Comparing means between >2 groups
Analysis of Variance (ANOVA)
Comparing means between >2 groups
Analysis of Variance (ANOVA)
Comparing means between >2 groups
The ratio of variances (F-statistic)
\[ F = \frac{\text{Variance 1}}{\text{Variance 2}} \]
- Can (in general) be used to test if the variances are equal between sources of variance
- \(F=1\) if variances are equal
- \(F\) is very low if variance 1 < variance 2
- \(F\) is very high if variance 1 > variance 2
Comparing means between >2 groups
Analysis of Variance (ANOVA)
\[ F = \frac{\text{Mean variance between-group}}{\text{Mean variance within-group}} \]
- If \(F\) is very big, more likely that means are different
Comparing means between >2 groups
Analysis of Variance (ANOVA)
- If you want to know if >2 groups differ in their means, use F-statistic
- Null hypothesis
- The means of all groups are the same
- Mean A == Mean B == Mean C
- Alternative hypothesis
- The means of at least one group differ from the global mean
Comparing means between >2 groups
Analysis of Variance (ANOVA)
Different from a hypothesised value?
Different from a hypothesised value?
Continuous variable
- Is the mean
ovipositor_length_mmin theheterophyllumhost race different from 1.78 mm? - Confidence interval approach
- Hypothesis testing approach
Different from a hypothesised value?
Continuous variable
Observed difference:
Different from a hypothesised value?
Continuous variable (confidence interval approach)
Different from a hypothesised value?
Continuous variable (confidence interval approach)
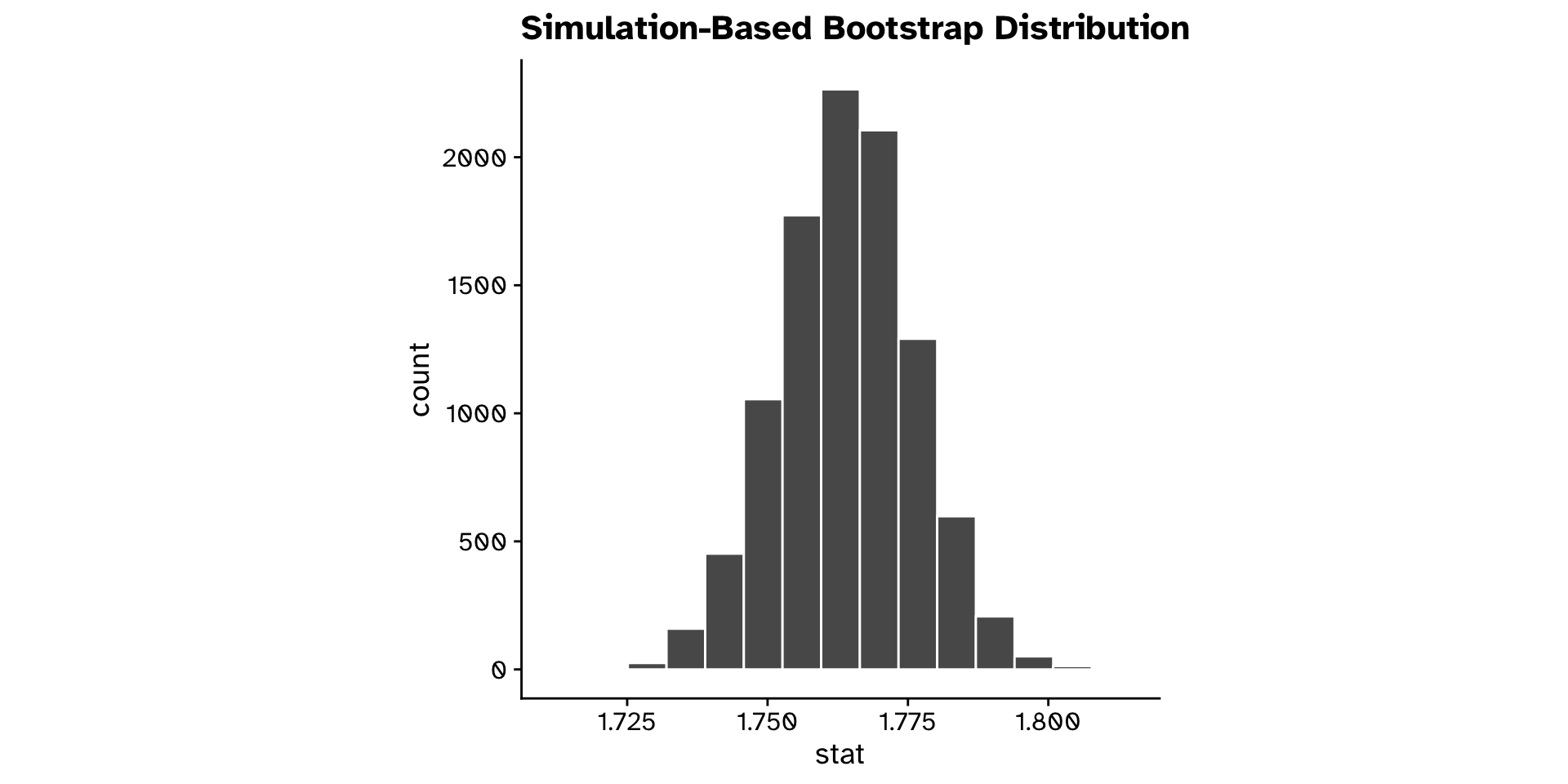
Different from a hypothesised value?
Continuous variable (confidence interval approach)
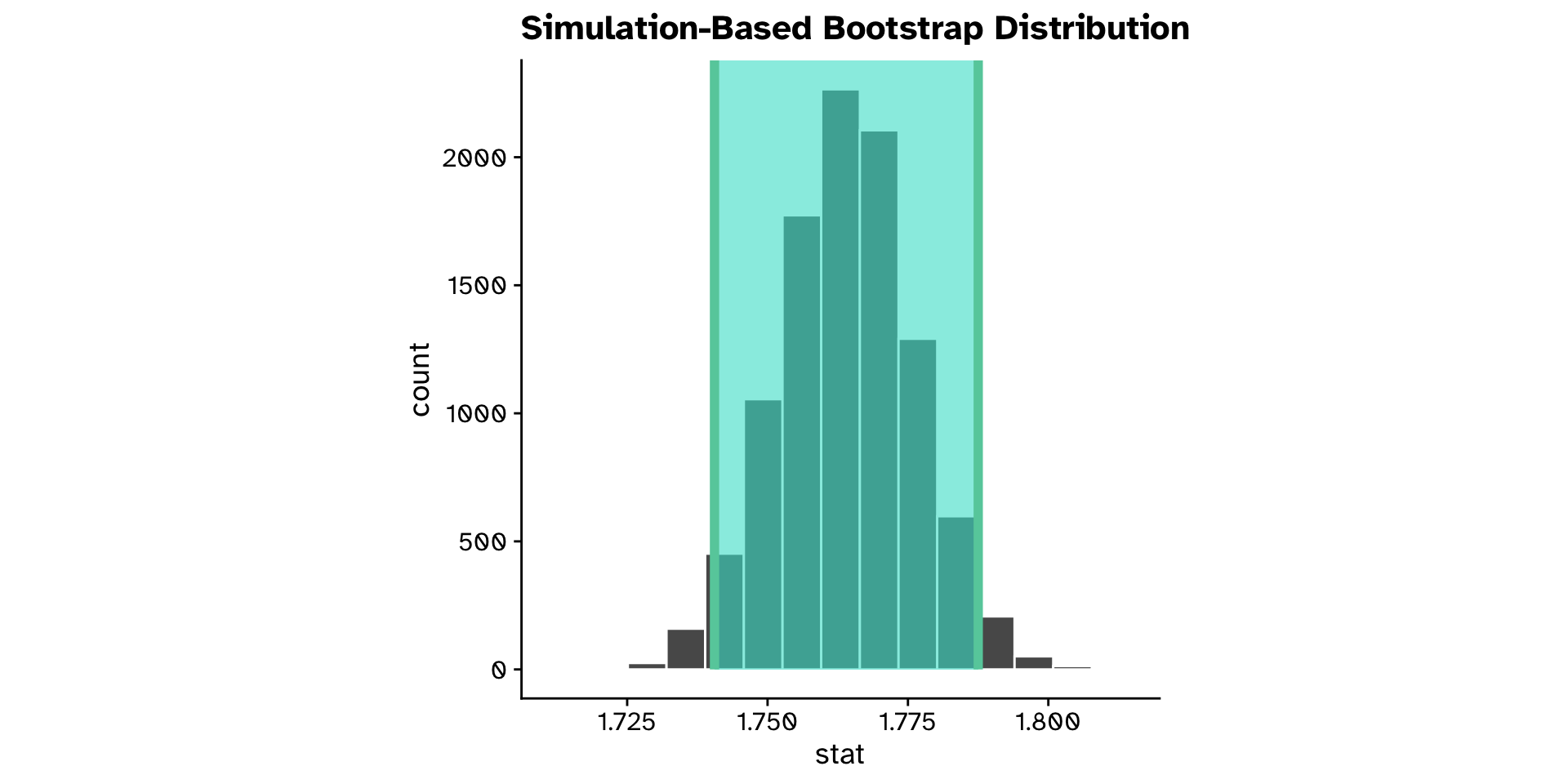
Different from a hypothesised value?
Continuous variable (confidence interval approach)
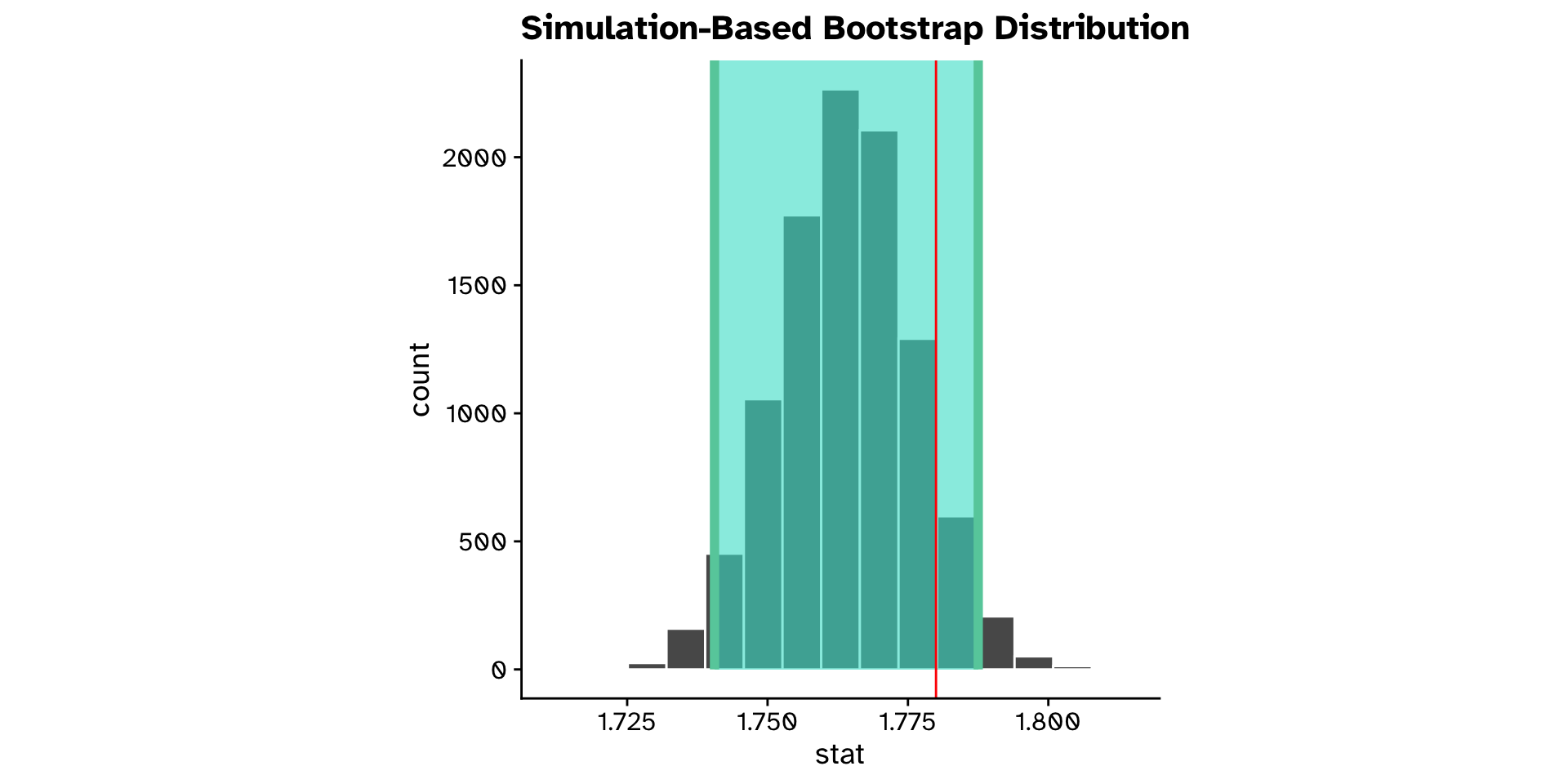
Different from a hypothesised value?
Continuous variable (confidence interval approach)
- Is the mean
ovipositor_length_mmin theheterophyllumhost race different from 1.78 mm?- Observed: 1.764 mm
- 95% confidence interval: 1.74 - 1.79 mm
- True mean is likely in this range
- Hypothesised value (1.78 mm) is also in the range
- We are not so confident that the true mean is not 1.78 mm
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
- Is the mean
ovipositor_length_mmin theheterophyllumhost race different from 1.78 mm?
01:30
Think 30 sec, discuss 60 sec
What is our null and alternative hypothesis?
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
- How do we get a null distribution?
- Permuting is not an option here
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
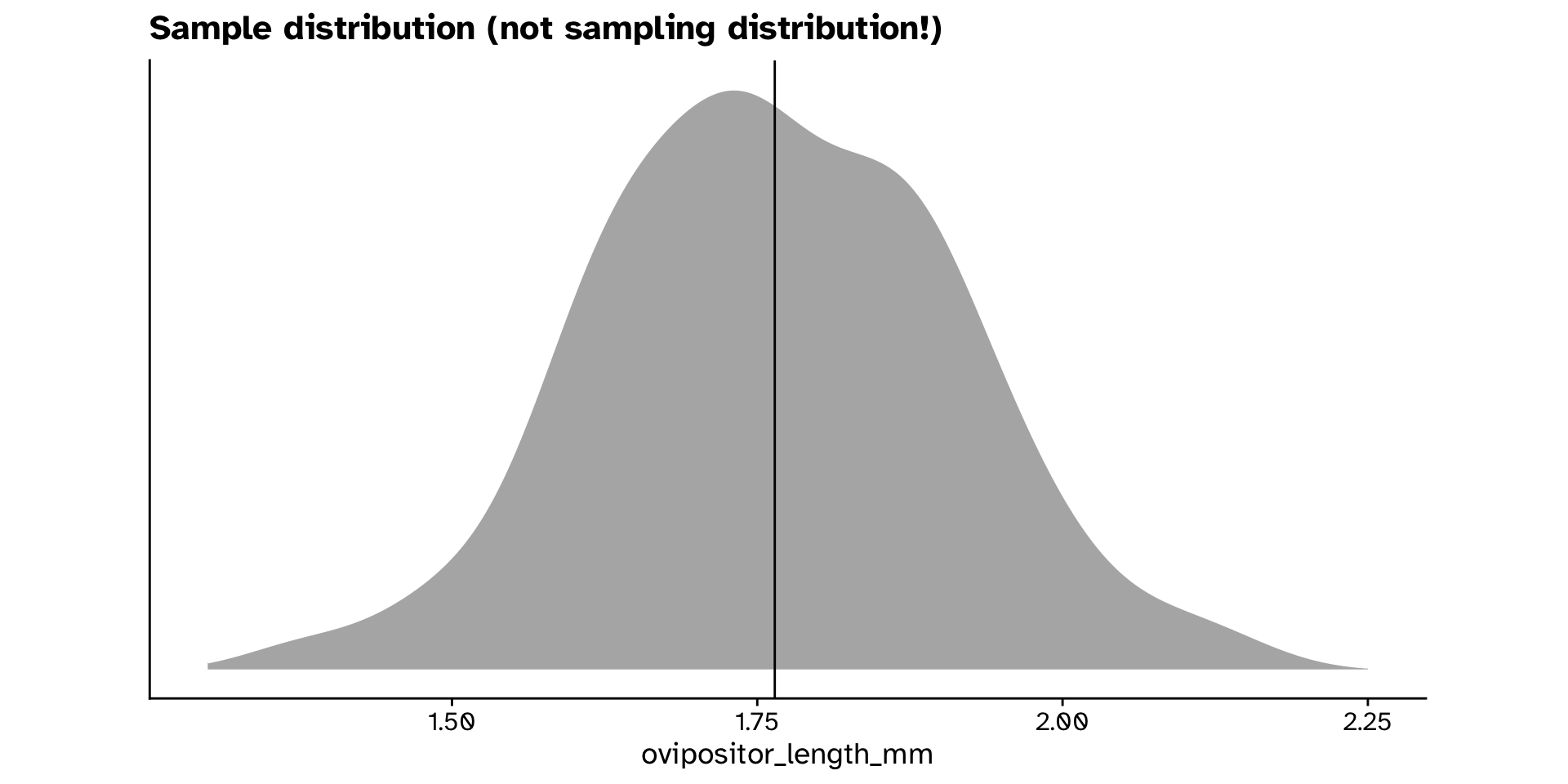
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
- Bootstrap resample from our new dataset that is compatible with the null hypothesis
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
- Bootstrap resample from our new dataset that is compatible with the null hypothesis
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
- Compare with observed value
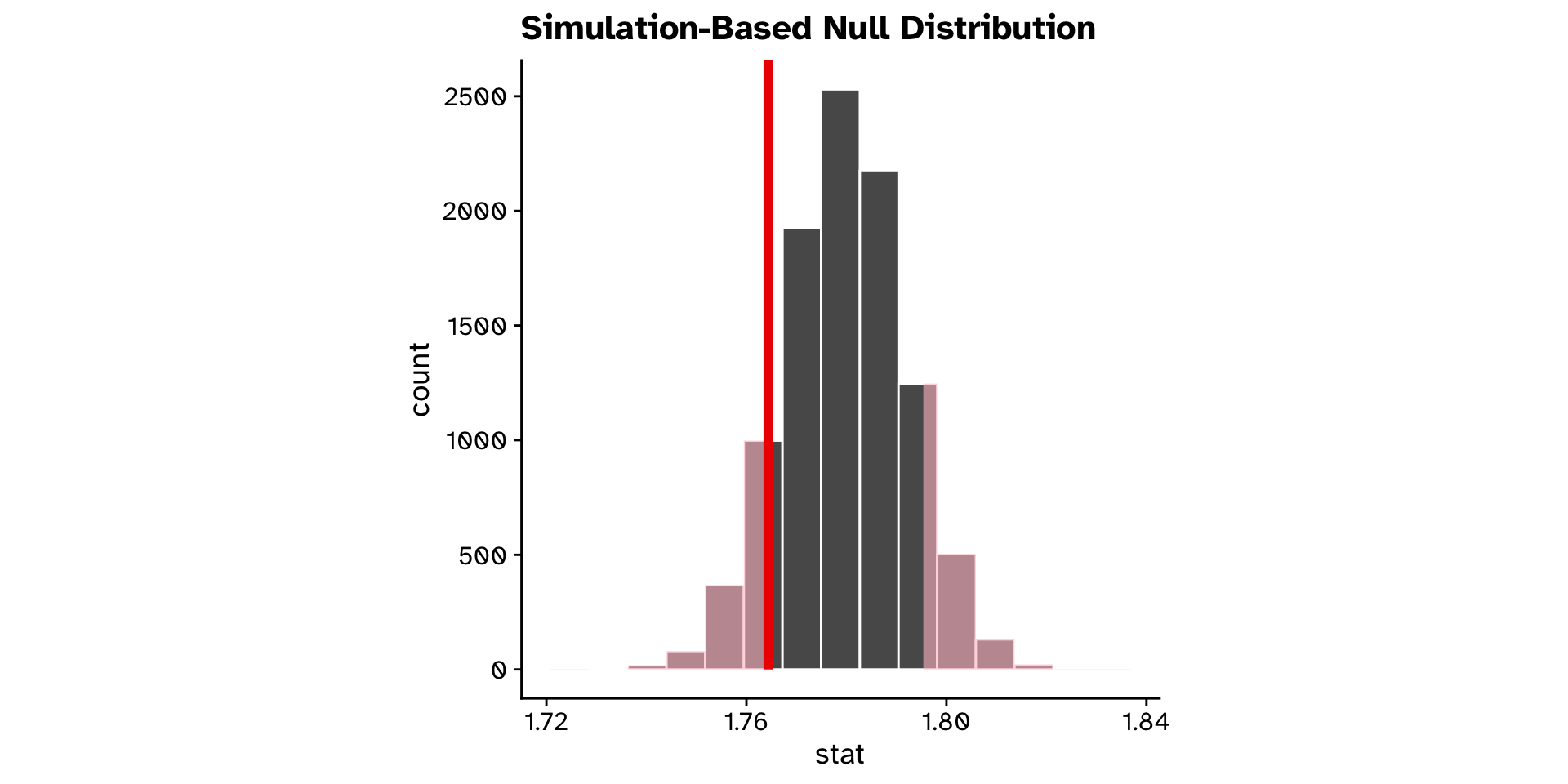
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
Different from a hypothesised value?
Continuous variable (hypothesis testing approach)
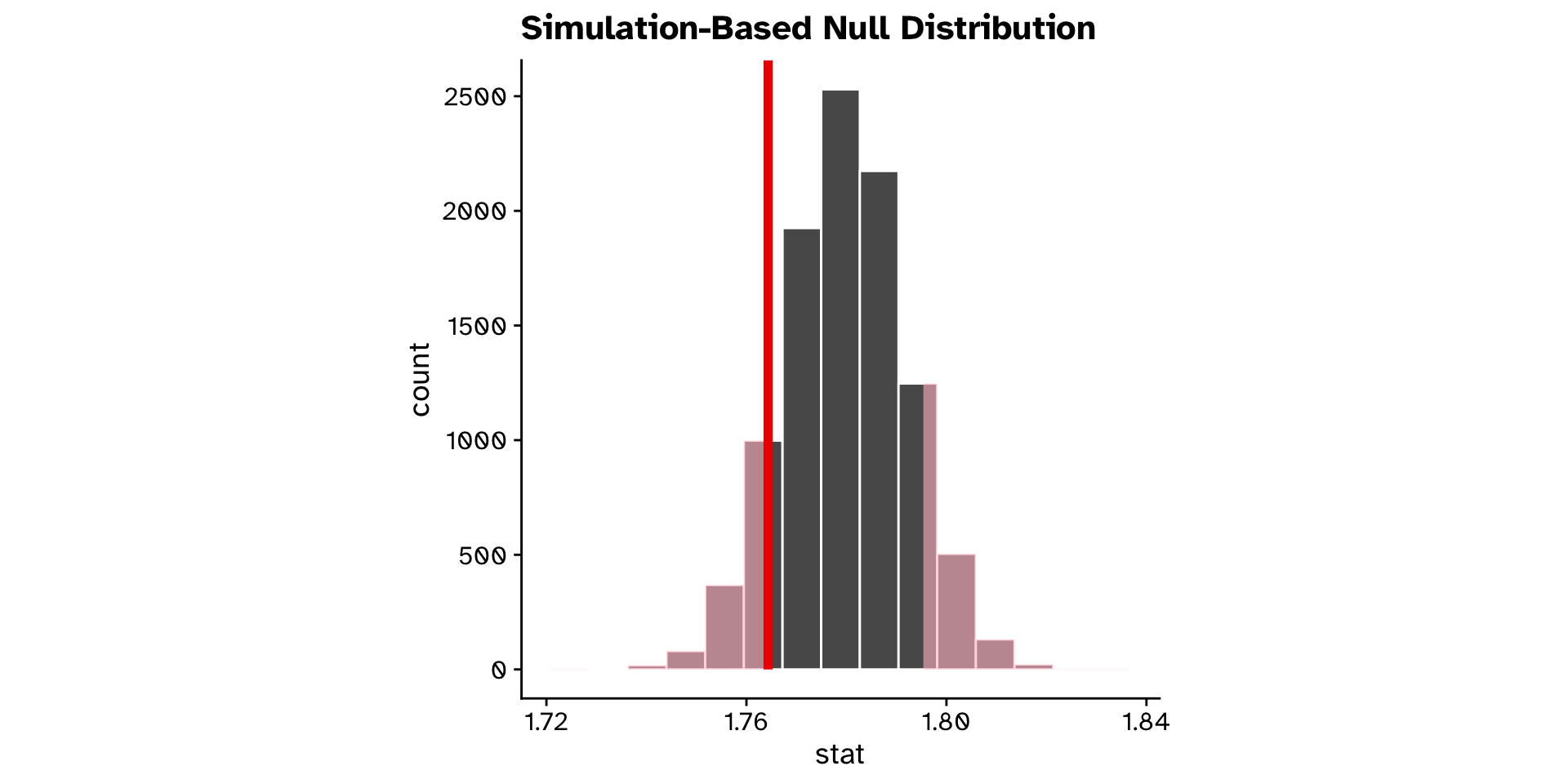
- Is the mean
ovipositor_length_mmin theheterophyllumhost race different from 1.78 mm?- Observed: 1.764 mm
- If the true mean was 1.78 mm, probability to observe 1.764 mm or a value more extreme is 0.2 (20% chance)
Categorical data
Tests of proportion
Tests of proportion
Is a proportion different from a hypothesised value?
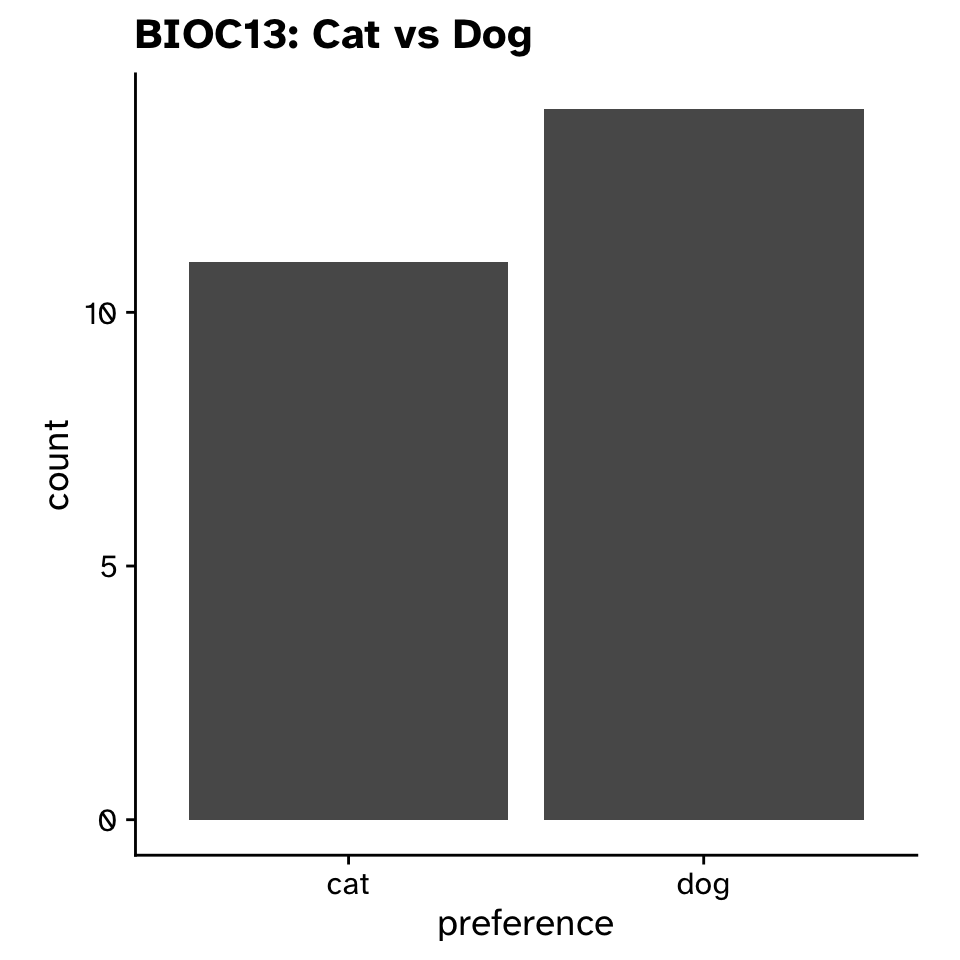
- In Sweden, 58% prefer dogs (according to a survey of 2000 people by Folksam)
- Do our preferences differ from this?
- Does the proportion of biology students who prefer dogs differ from 0.58?
Tests of proportion
Is a proportion different from a hypothesised value?
Tests of proportion
Is a proportion different from a hypothesised value?
Calculate the test statistic:
Tests of proportion
Is a proportion different from a hypothesised value? (CI)
Tests of proportion
Is a proportion different from a hypothesised value? (CI)
Tests of proportion
Is a proportion different from a hypothesised value? (CI)
Tests of proportion
Is a proportion different from a hypothesised value? (Hyp. test)
Tests of proportion
Is a proportion different from a hypothesised value? (Hyp. test)
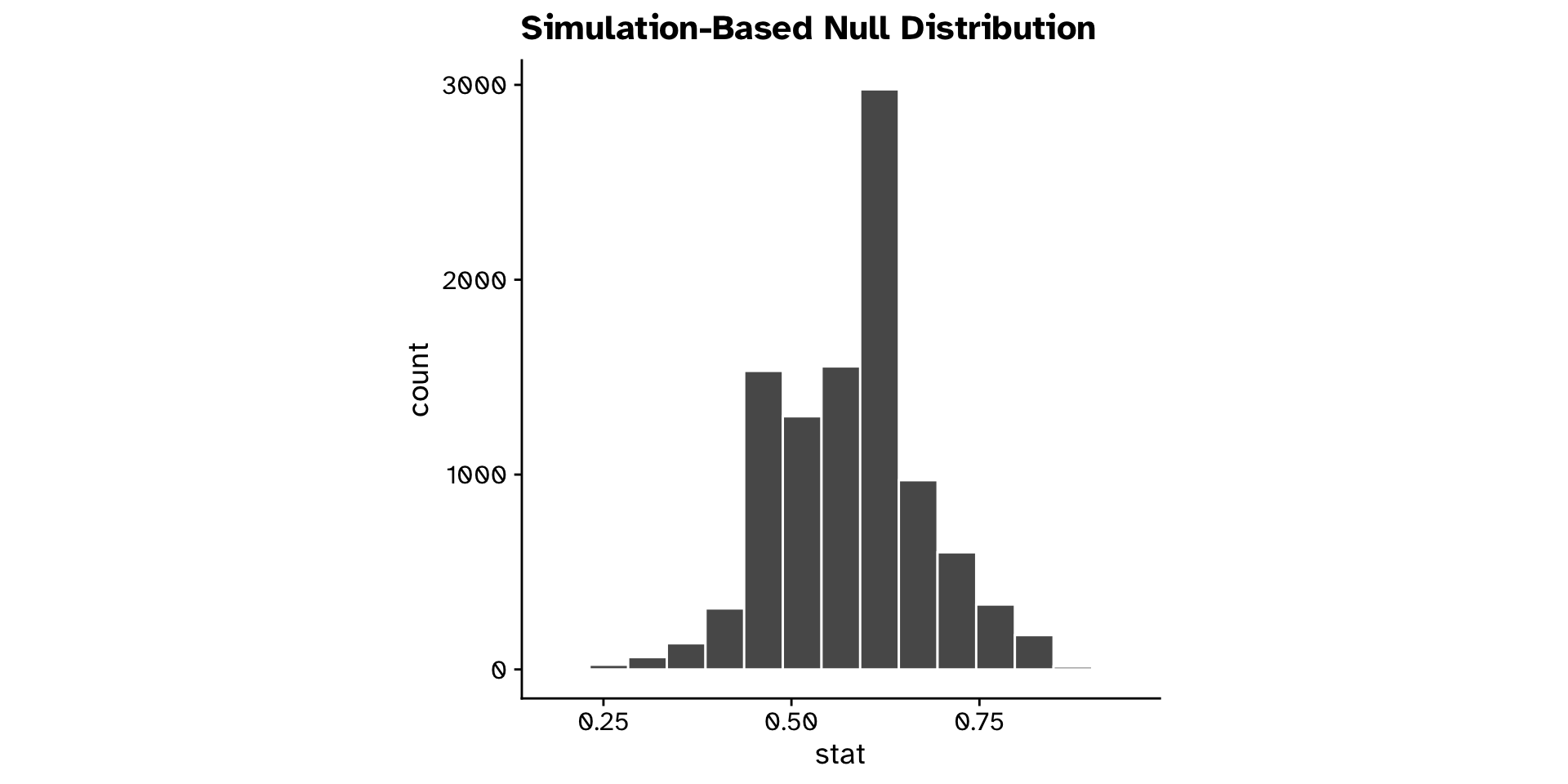
Tests of proportion
Is a proportion different from a hypothesised value? (Hyp. test)
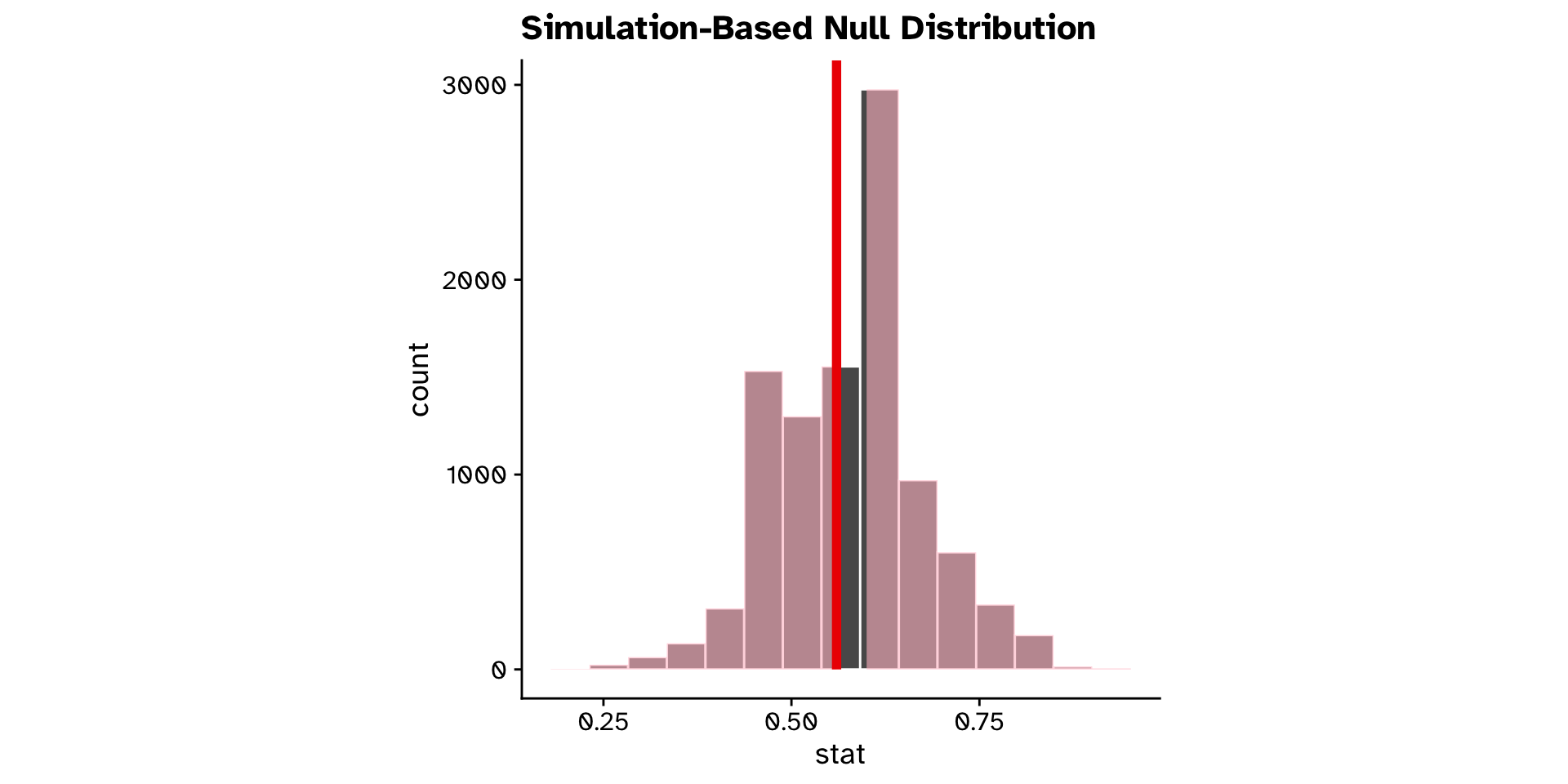
Tests of proportion
Is a proportion different from a hypothesised value? (Hyp. test)
Tests of proportion, but more
Are 2 or more distributions different?
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
- Exactly what we have just done, but we extend it beyond binary (yes/no, cat/dog) data
- Similar to how F-statistic allows for diff in means for many groups
- \(\chi^2\) allows for difference in proportions for many categories
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
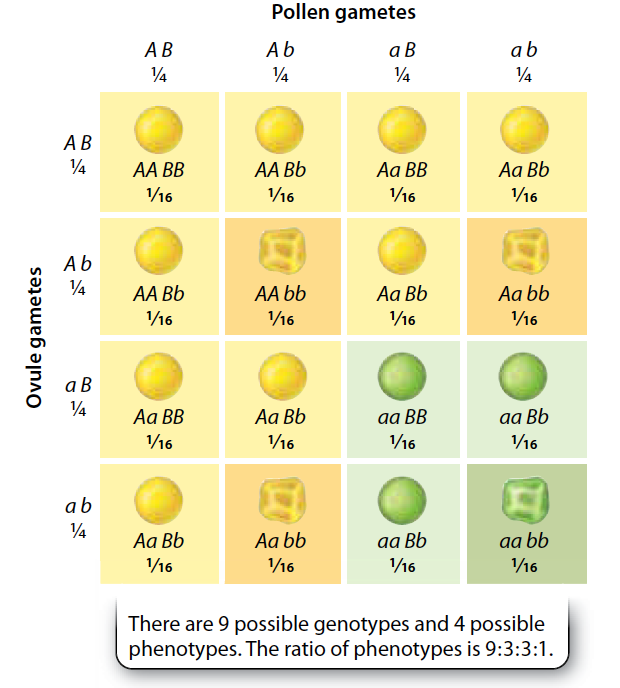
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
# A tibble: 120 × 1
phenotype
<chr>
1 A-B-
2 A-B-
3 A-B-
4 A-B-
5 A-B-
6 A-B-
7 A-B-
8 A-B-
9 A-B-
10 A-B-
# ℹ 110 more rows\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
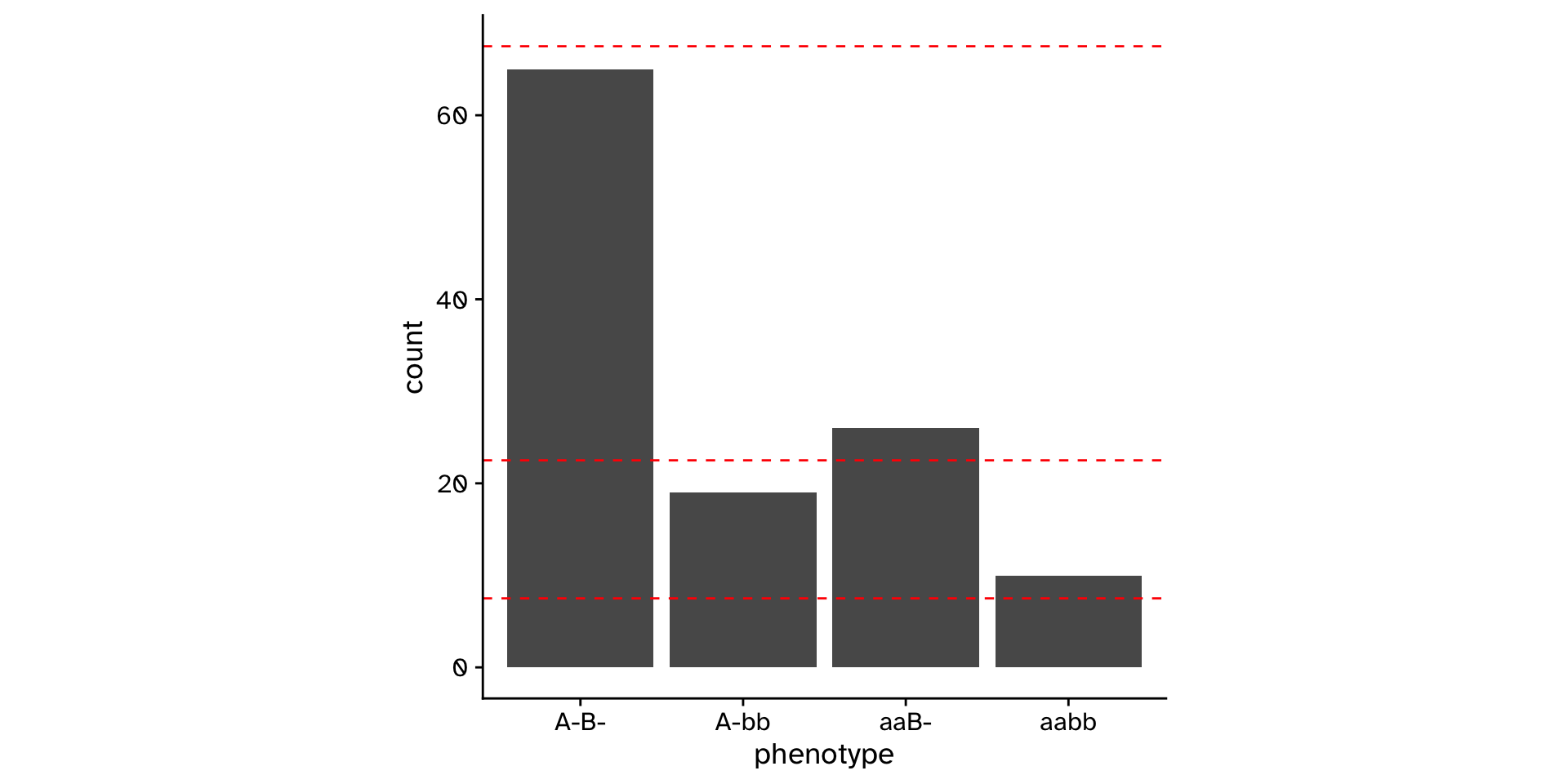
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
\[ \chi^2 = \sum \frac{(Observed_i - Expected_i)^2}{Expected_i} \]
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
- Null hypothesis:
- The sample came from the hypothesised distribution
- The sample distribution is not different from the hypothesised distribution
- Alternative hypotheis:
- The sample came from a different distribution to the one hypothesised
- The sample distribution is different from the hypothesised distribution
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
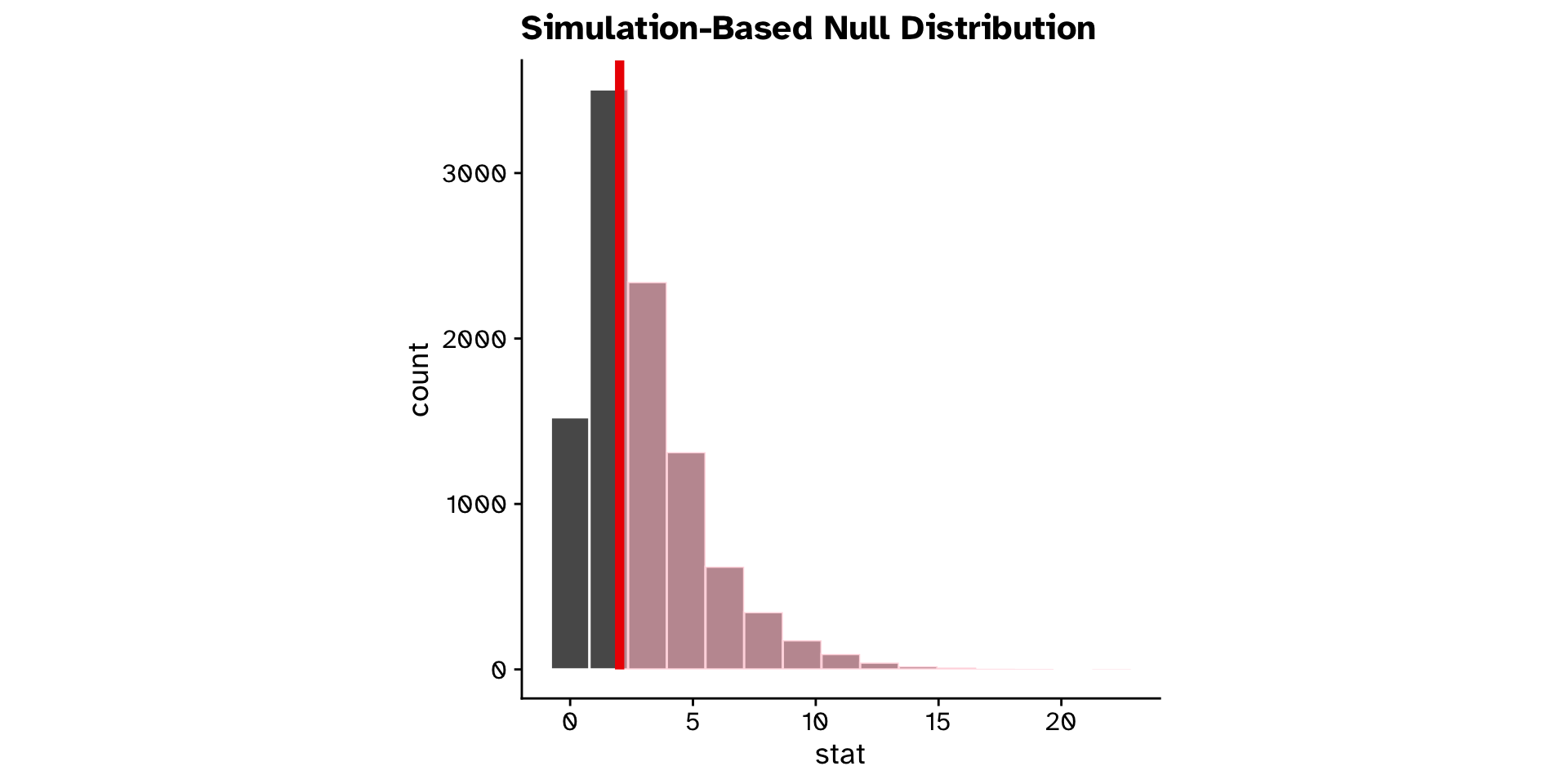
\(\chi^2\) Goodness of fit
Does the observed data differ from an expected distribution?
Are two categorical variables associated with each other?
\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
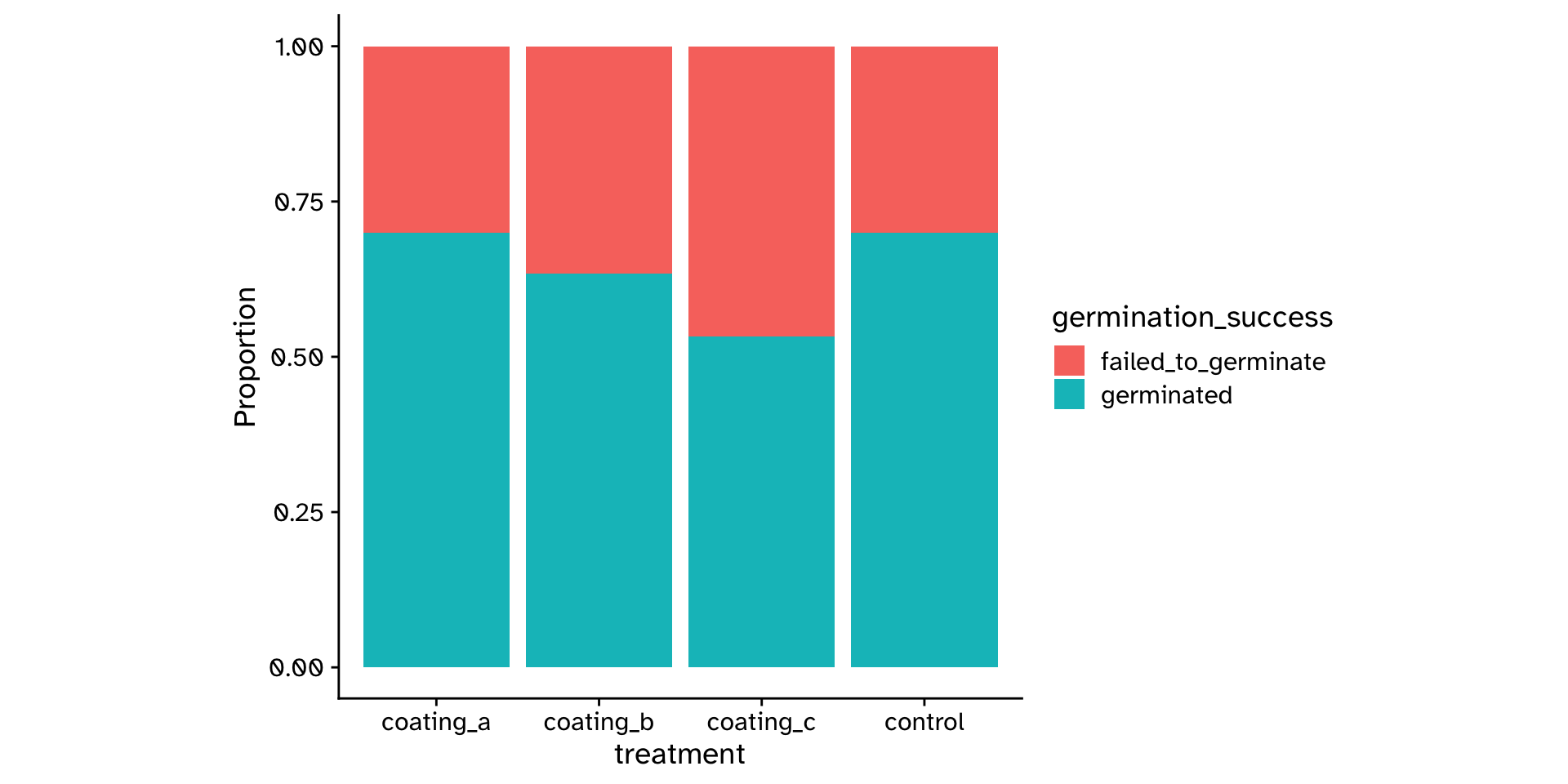
\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
# A tibble: 120 × 2
treatment germination_success
<chr> <chr>
1 coating_a germinated
2 coating_a germinated
3 coating_a germinated
4 coating_a failed_to_germinate
5 coating_a germinated
6 coating_a germinated
7 coating_a germinated
8 coating_a germinated
9 coating_a germinated
10 coating_a germinated
# ℹ 110 more rows\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
- Null hypothesis:
- The two categorical variables are not associated with each other
- The two categorical variables are independent
- Alternative hypothesis:
- The two categorical variables are associated with each other
- The two categorical variables are not independent
\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
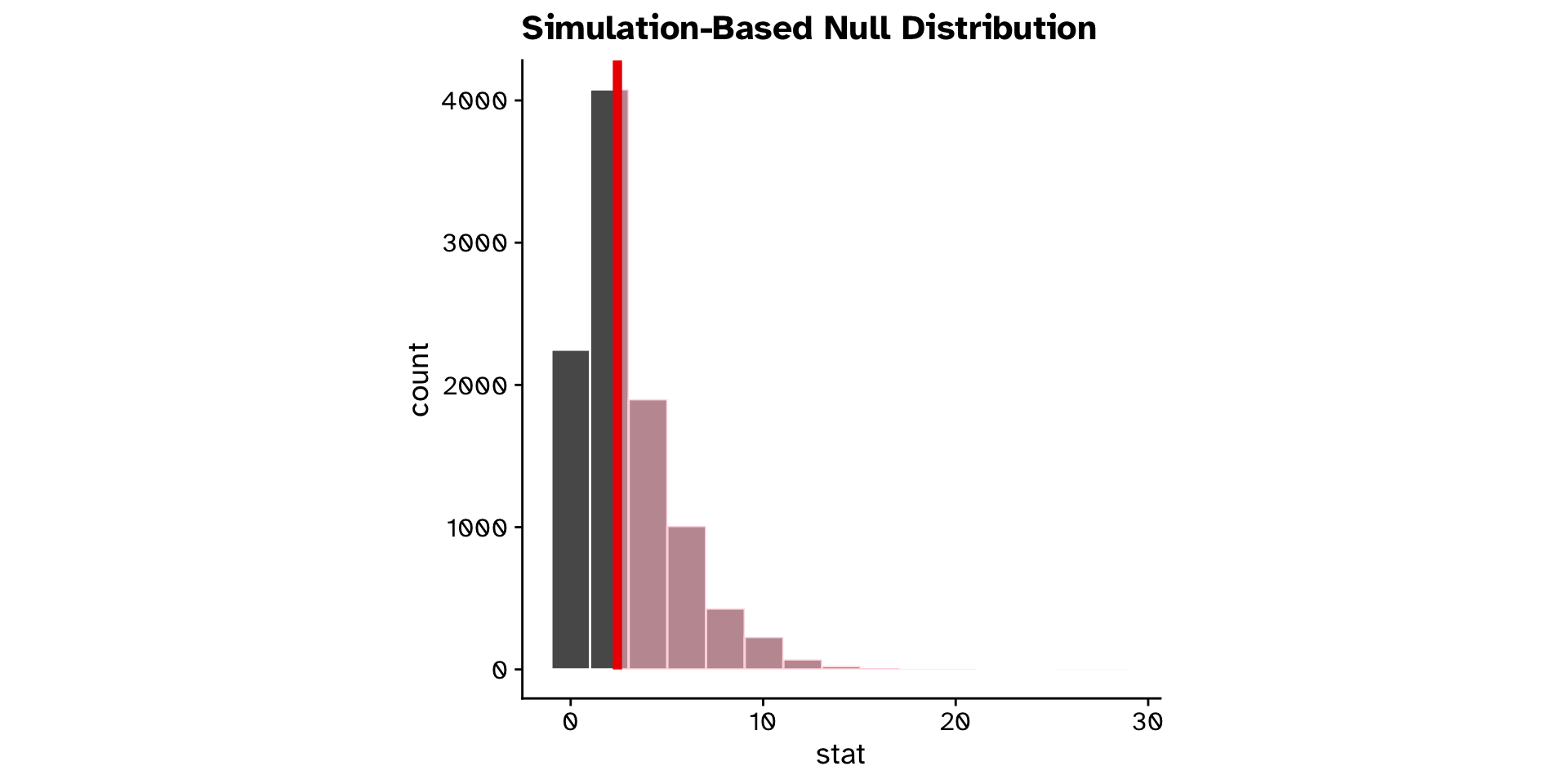
\(\chi^2\) Test of independence
Are two categorical variables associated with each other?
Correlation
Correlation
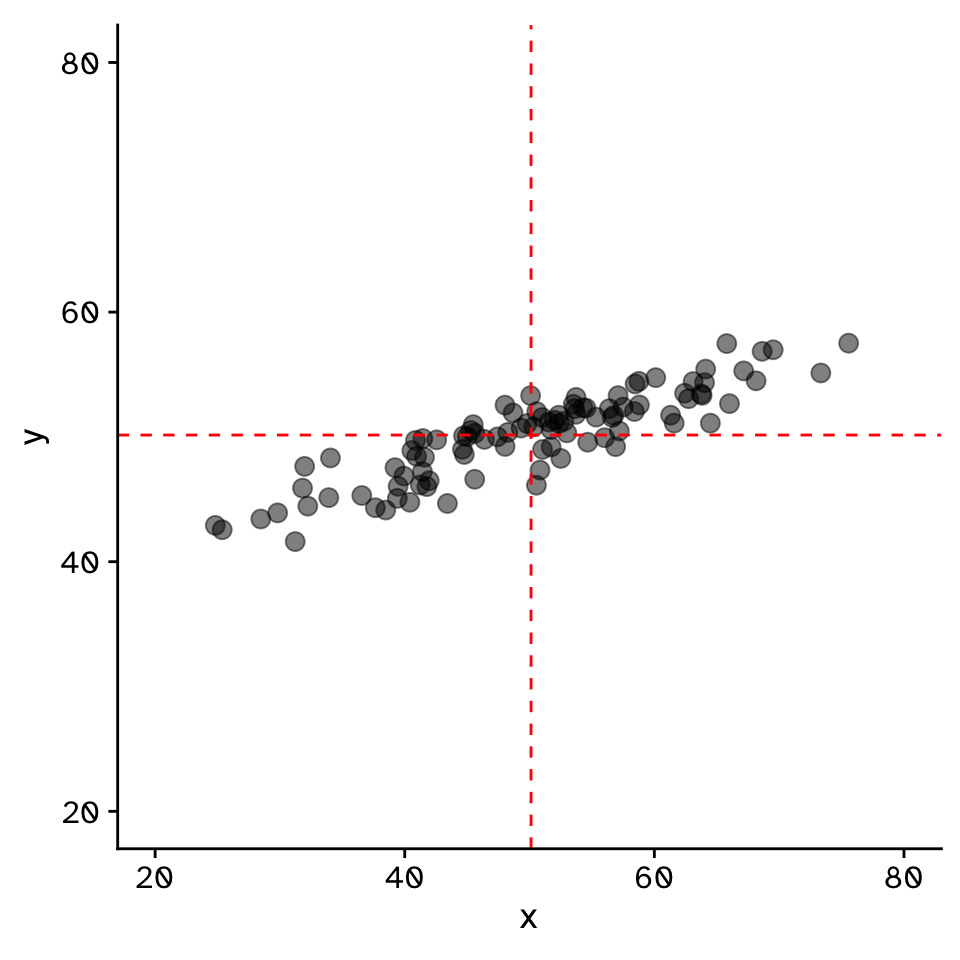
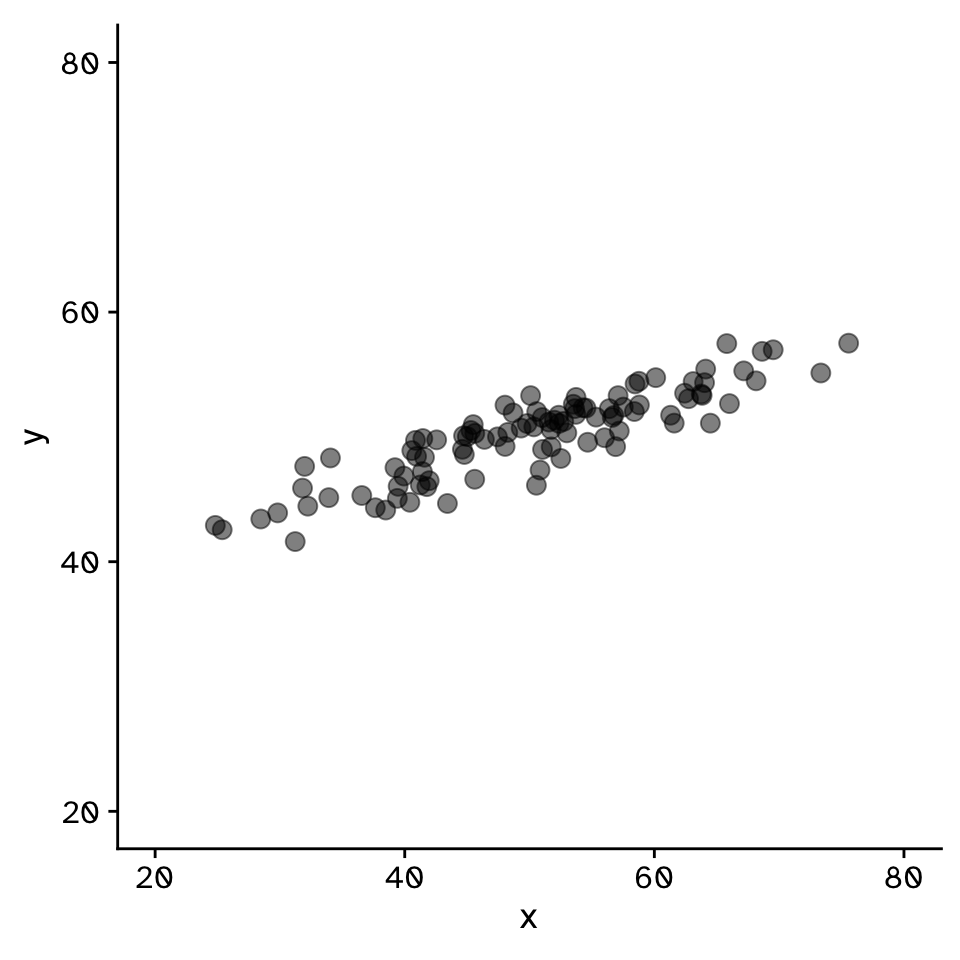
Do two continuous variables covary?
- Used to assess if two continuous variables are independent, or if they covary (linearly)
- We do not express one variable as a function of another:
- No “response” and “explanatory”
- Usually assumed that both variables are “effects of a common cause” (Sokal and Rohlf 1995)
- “Correlation does not mean causation”
- But you can measure a correlation between a cause and effect
Correlation
Do two continuous variables covary?
Correlation coefficient (Pearson):
\[ r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}} \]
\[ r = \frac{\text{Covariance}(x,y)}{\text{Standard deviation}(x) \times \text{Standard deviation}(y)} \]
\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]
Correlation
Do two continuous variables covary?
\[ r = \frac{\text{Cov}(x,y)}{\sigma_x \sigma_y} \]
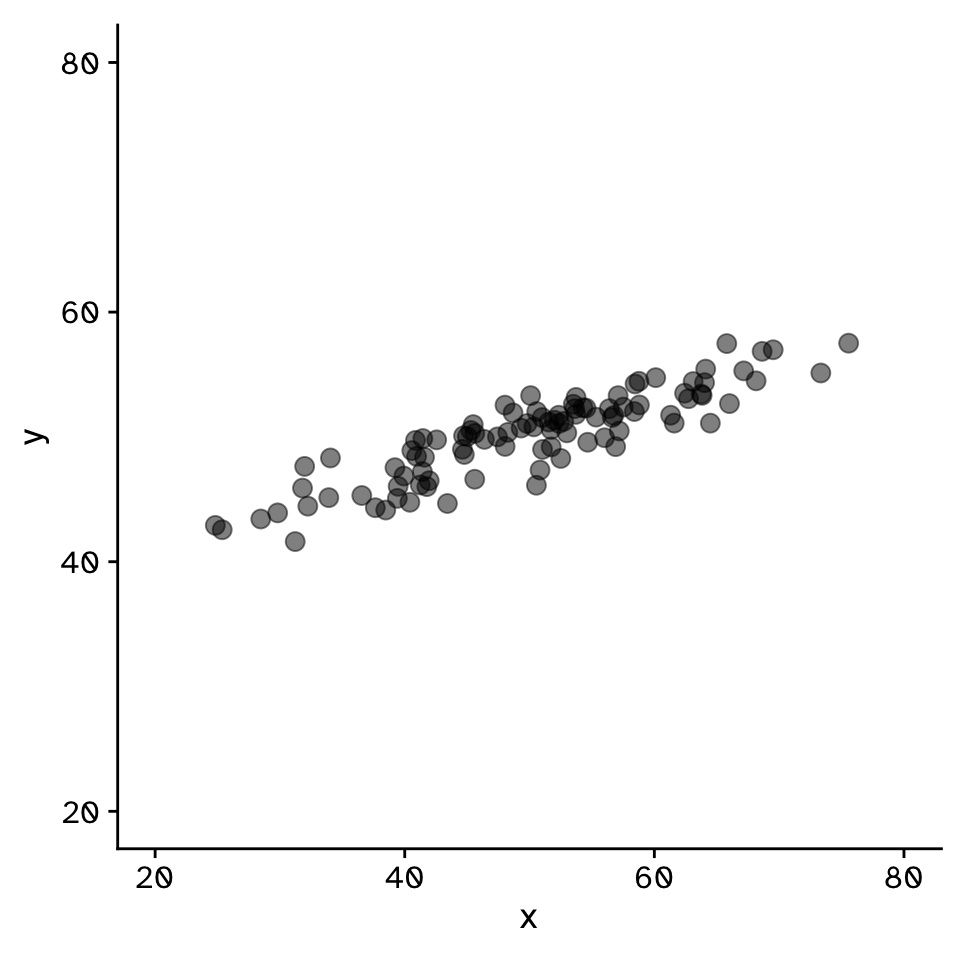
Correlation
Do two continuous variables covary?
Correlation
Do two continuous variables covary?
Correlation
Do two continuous variables covary?
Correlation
Do two continuous variables covary?
Correlation
Do two continuous variables covary?
Correlation
Do two continuous variables covary?
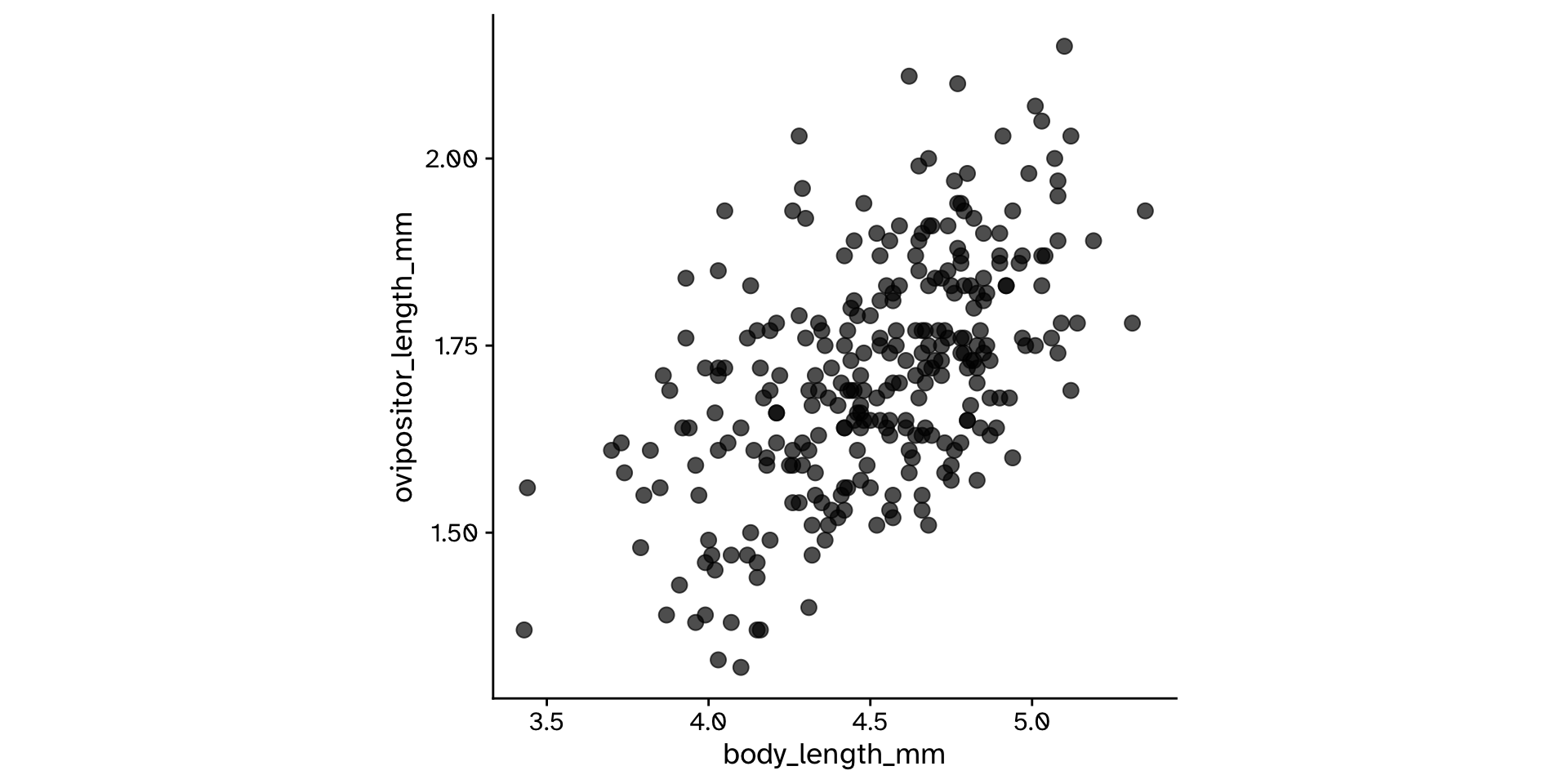
Correlation
Do two continuous variables covary?
Correlation
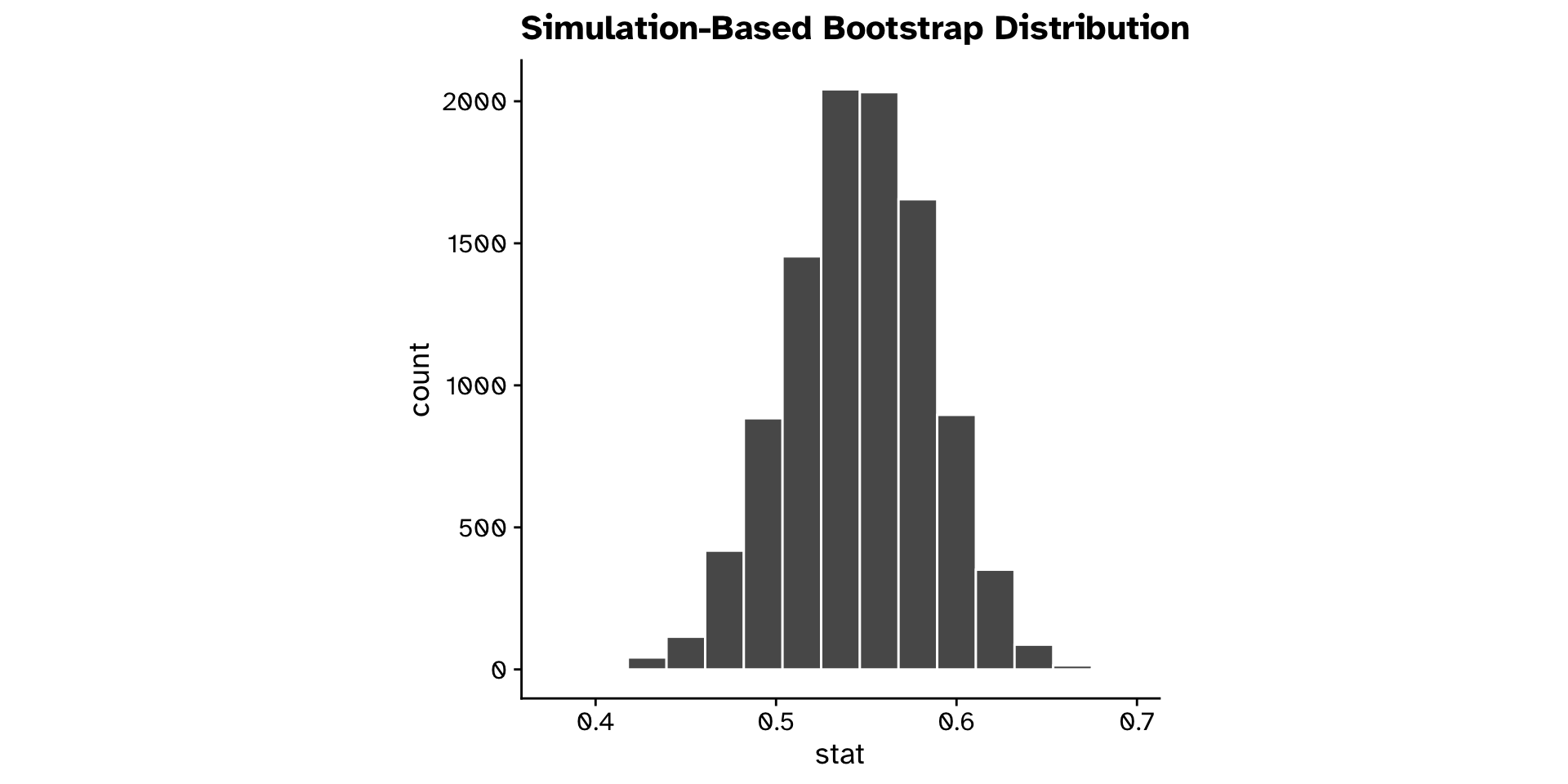
Do two continuous variables covary? (CI)
Correlation
Do two continuous variables covary? (CI)
Correlation
Do two continuous variables covary? (CI)
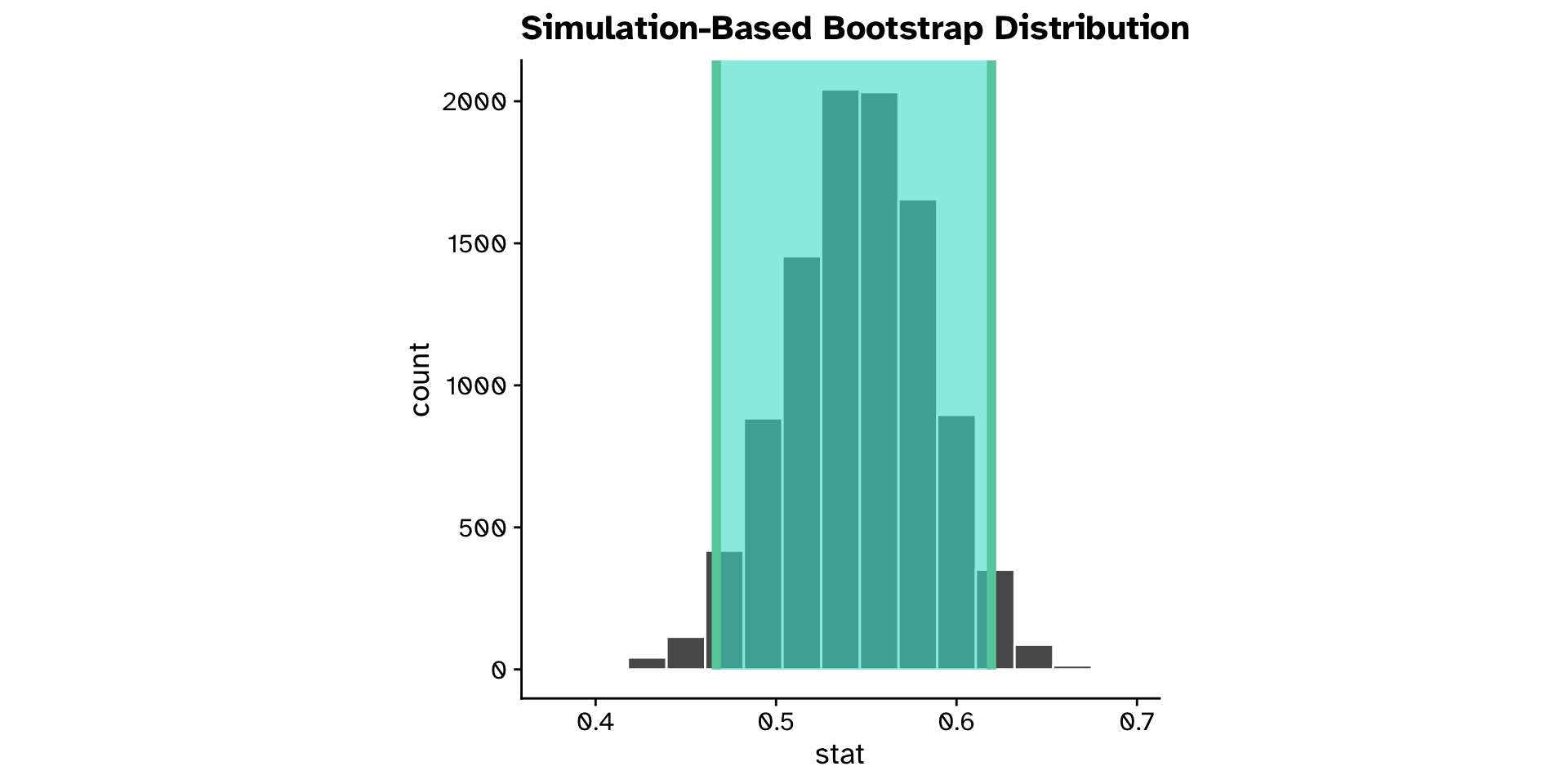
Correlation
Do two continuous variables covary? (Hyp. test)
Correlation
Do two continuous variables covary? (Hyp. test)
02:00
Think 30 sec, discuss 90 sec
What is our null and alternative hypothesis? How could we generate data compatible with the null?
Correlation
Do two continuous variables covary? (Hyp. test)
Correlation
Do two continuous variables covary? (Hyp. test)
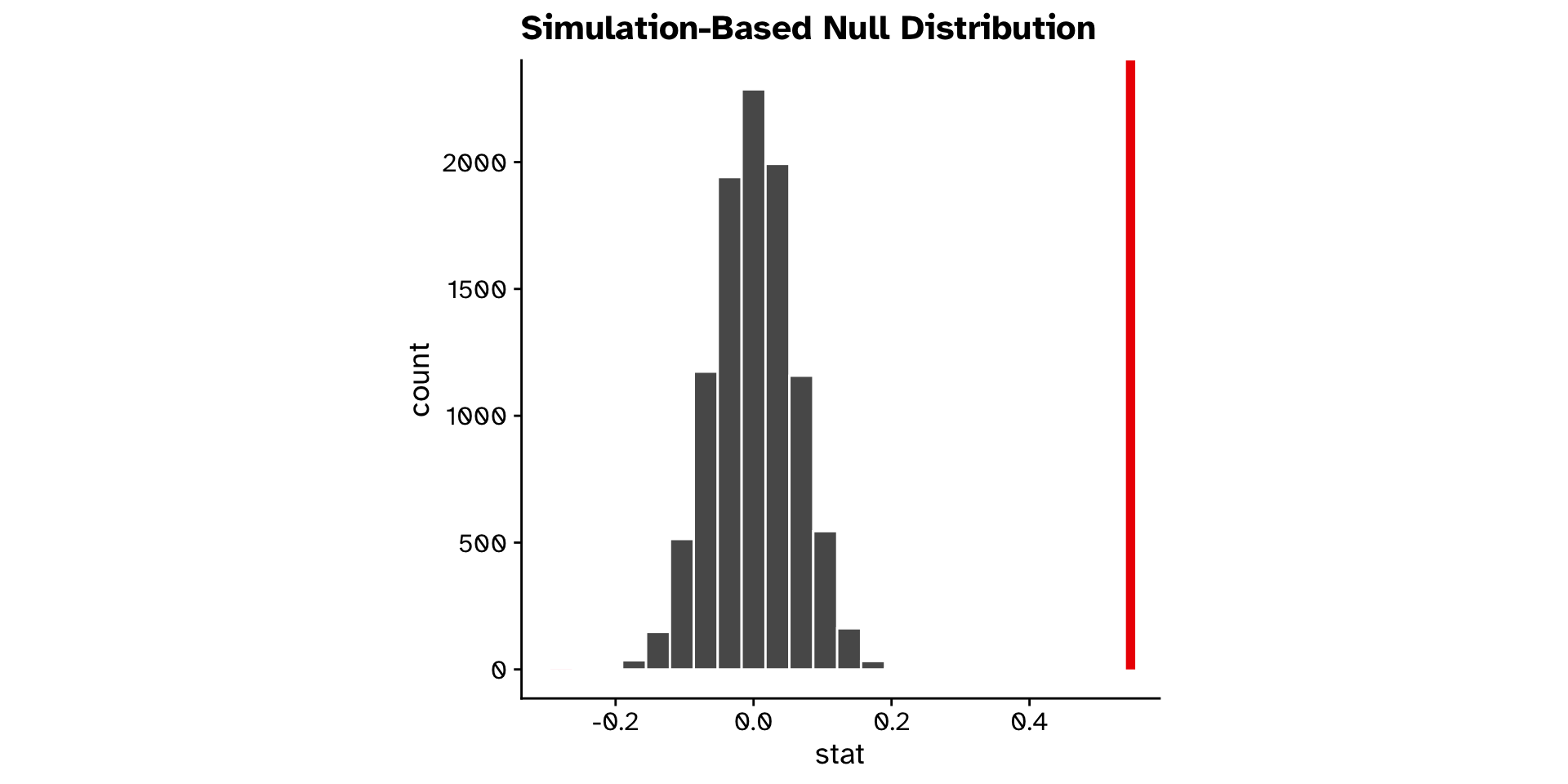
Regression
Regression
How does variable Y depend on variable X
- A mathmatical function describing the relationship between two continuous variables
- Y is dependant on X (the)
- Y is a function of X
- Predictive model
- Very powerful framework
Regression
How does variable Y depend on variable X
\[ y = \text{Slope}\times x + \text{Intercept} \]
\[ y = mx+c \]
\[ y = \beta_1x+\beta_0 \]
\[ y = \beta_0+\beta_1x+\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5 \]
Regression
How does variable Y depend on variable X
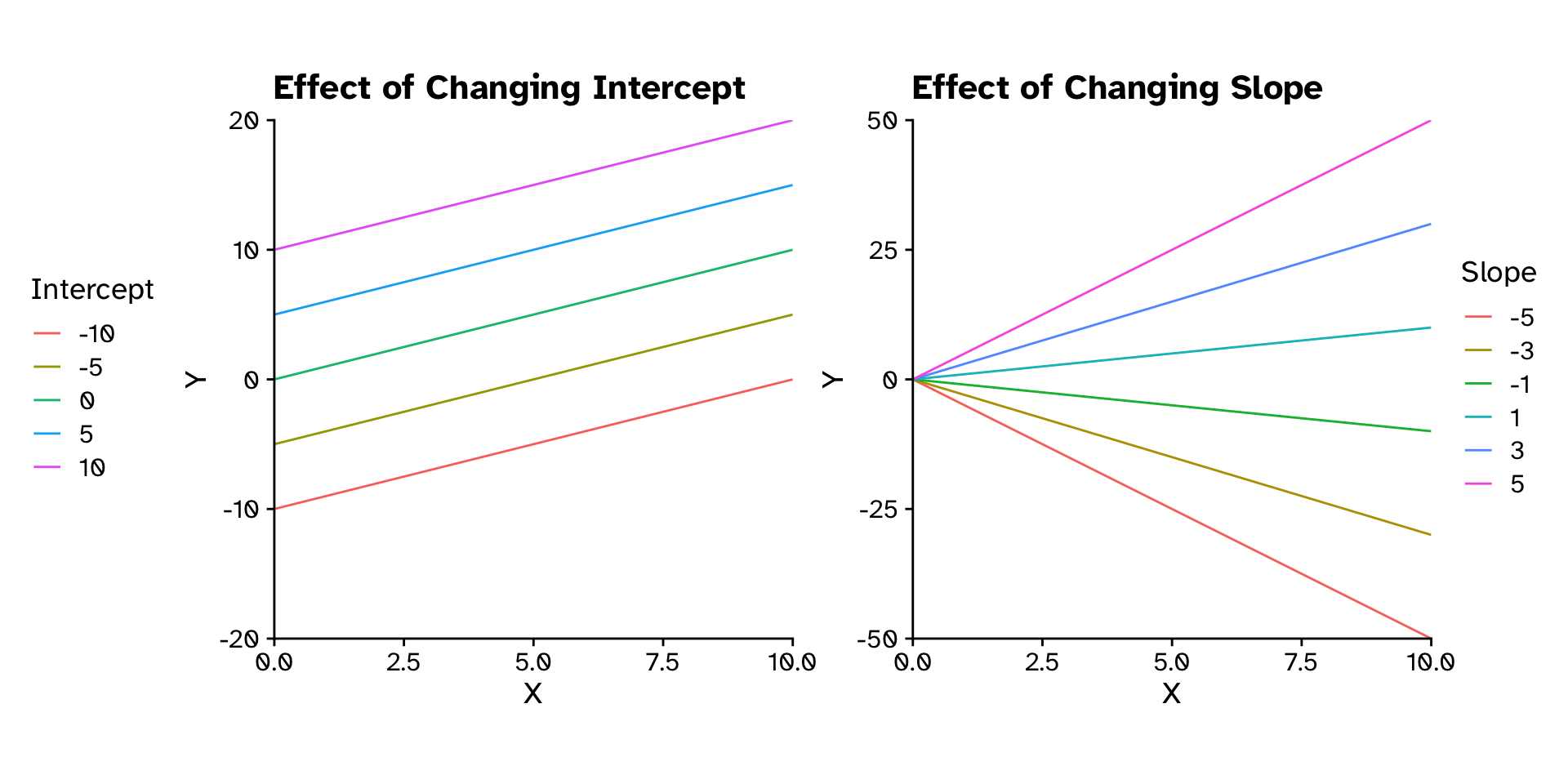
Regression
How does variable Y depend on variable X
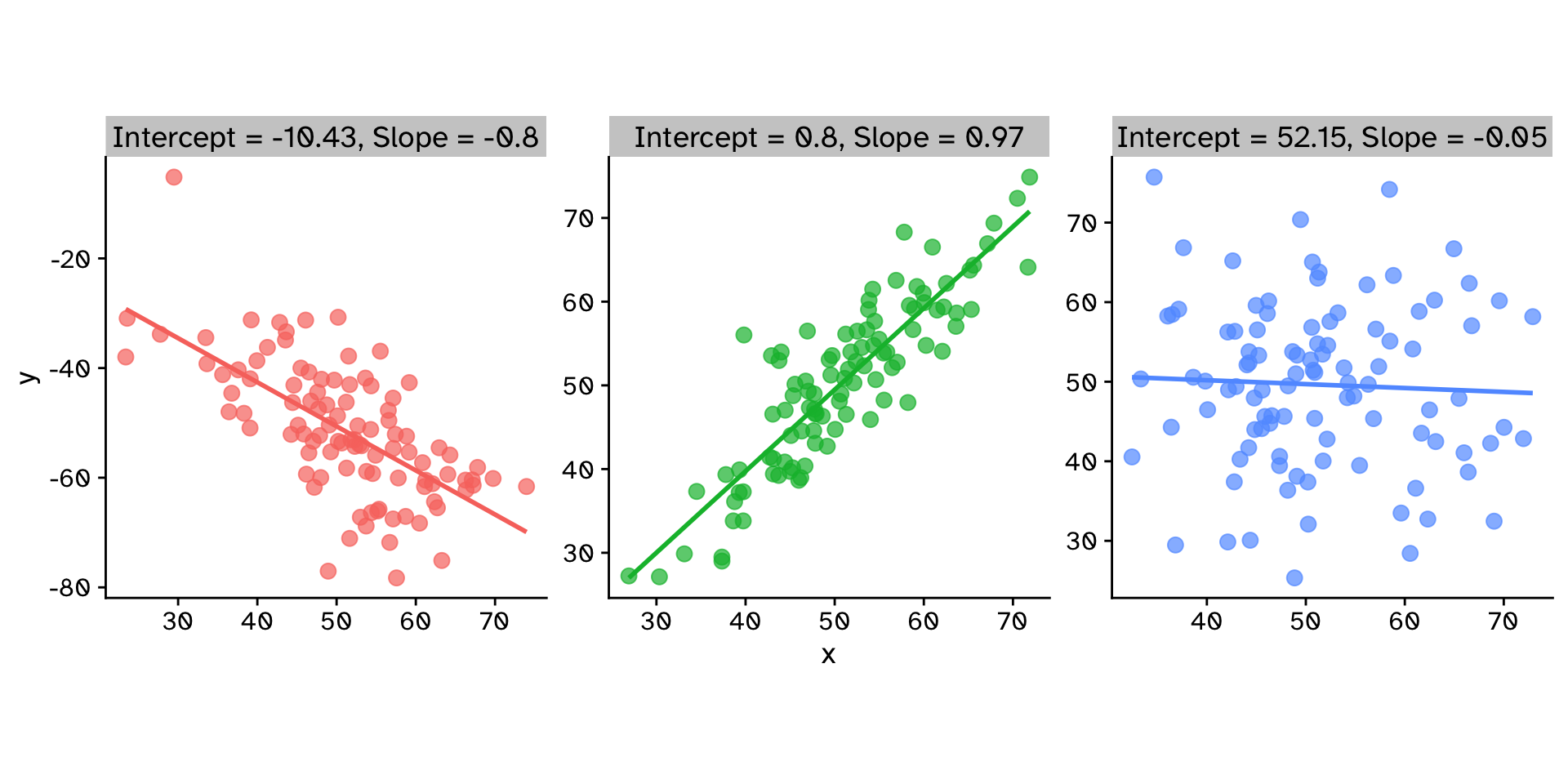
Regression
How does variable Y depend on variable X
- Example: For sexual selection to operate, an increase in mating success (number of mates) must result in an increase in reproductive success (number of offspring).
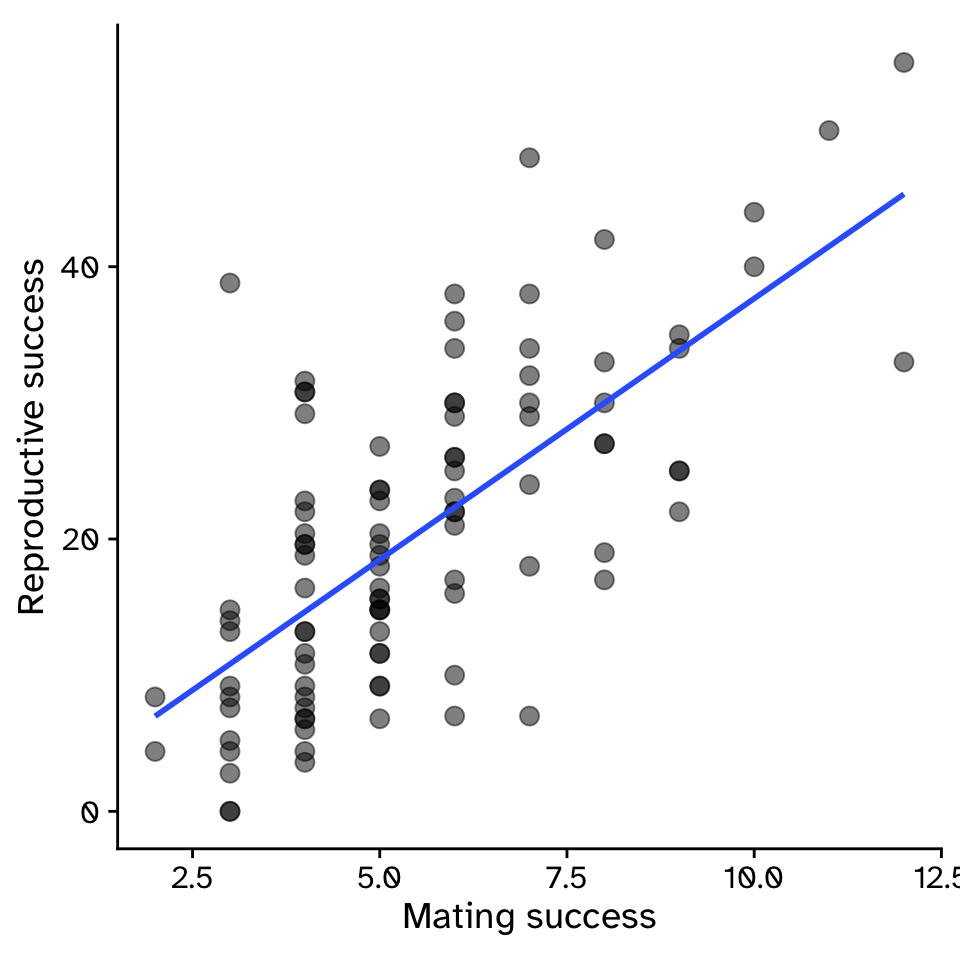
Regression
How does variable Y depend on variable X
\[ y = \beta_1x+\beta_0 \]
\[ y = 3.83x-0.68 \]
- \(\beta_1\) = strength of sexual selection
- For each additional mate, an individual (on average) gains \(\beta_1\) additional offspring
- For 5 mates (\(x=5\)):
- \(y = 3.83\times5-0.68\)
- \(y = 18.47\)
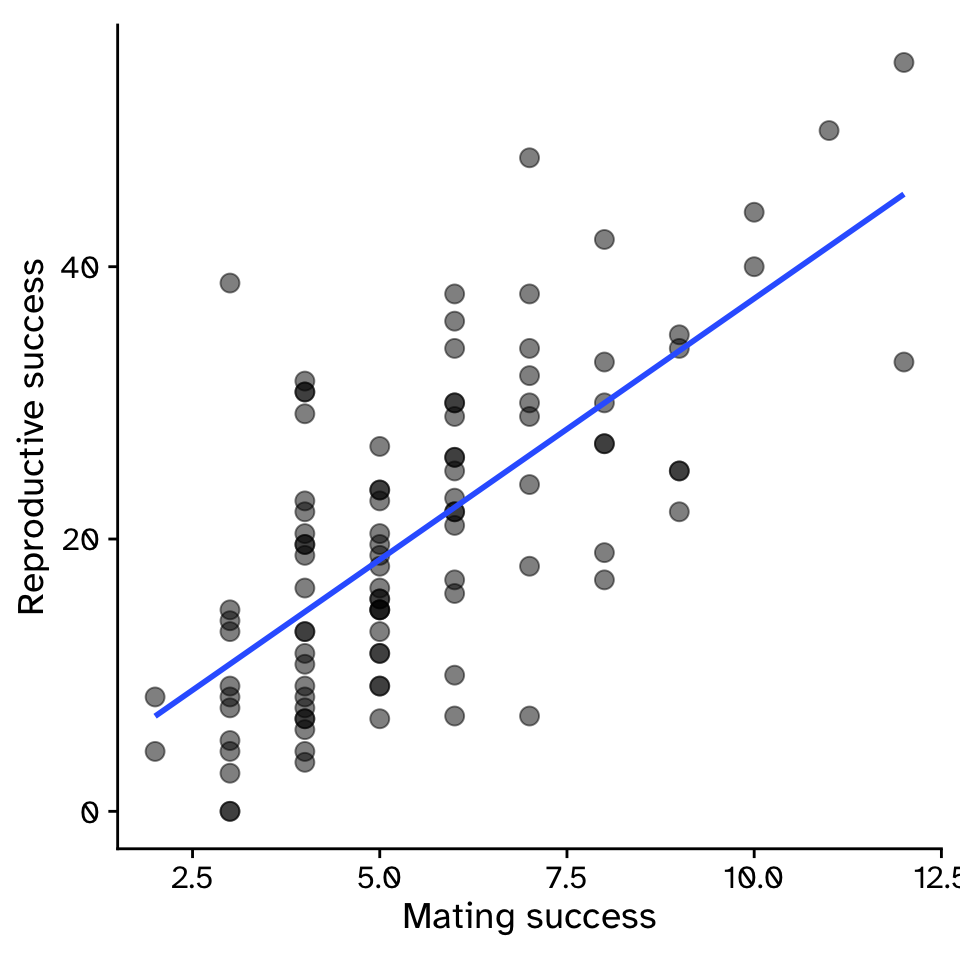
Regression
How does variable Y depend on variable X
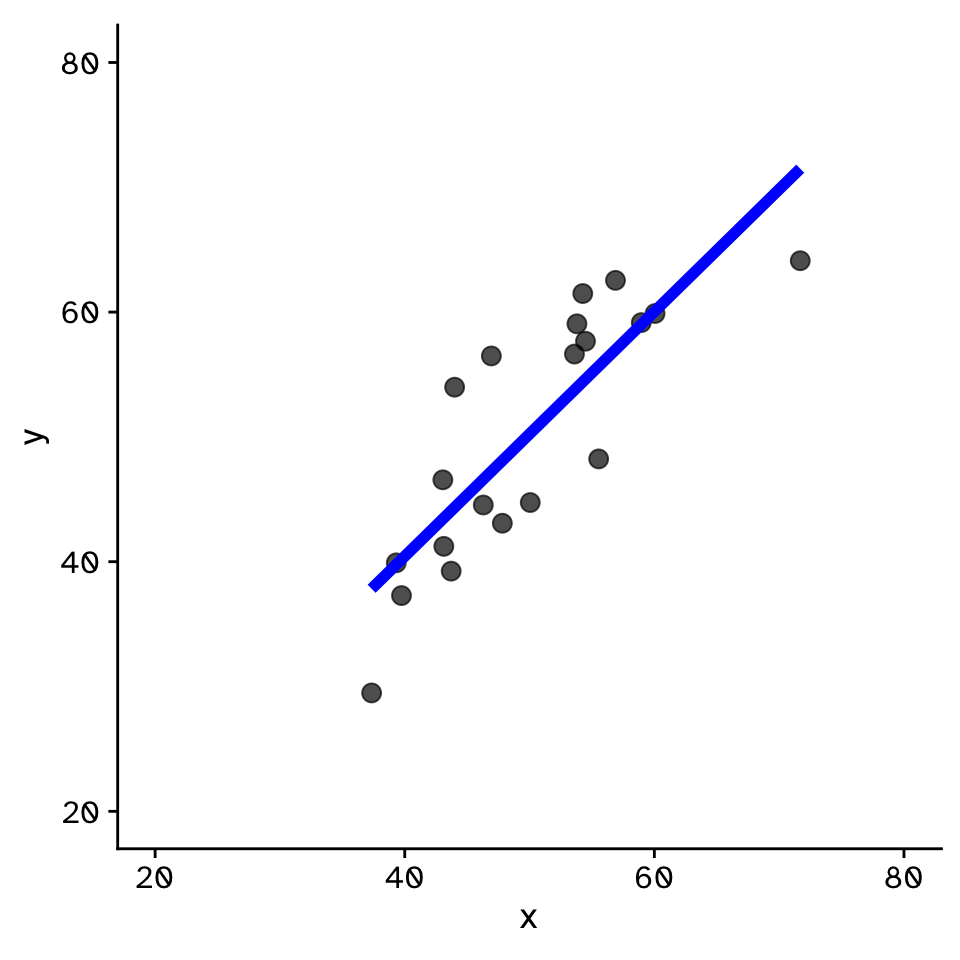
Regression
How does variable Y depend on variable X
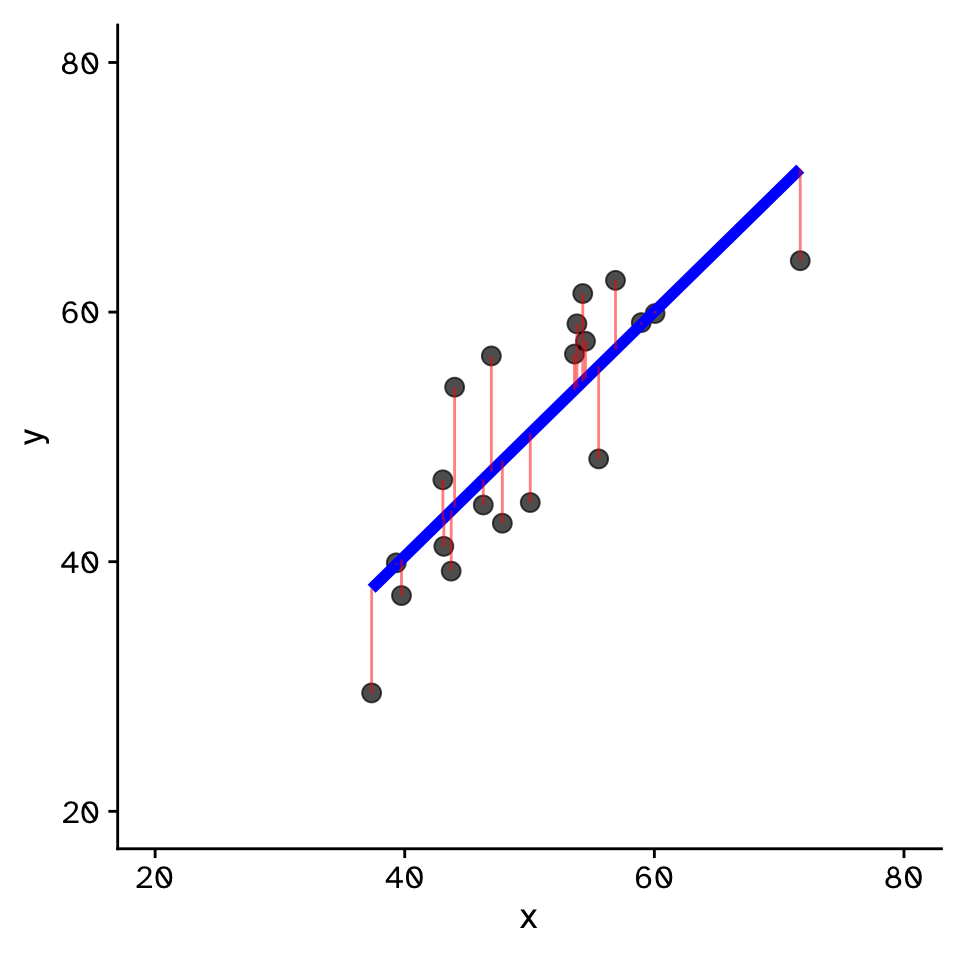
Regression
How does variable Y depend on variable X
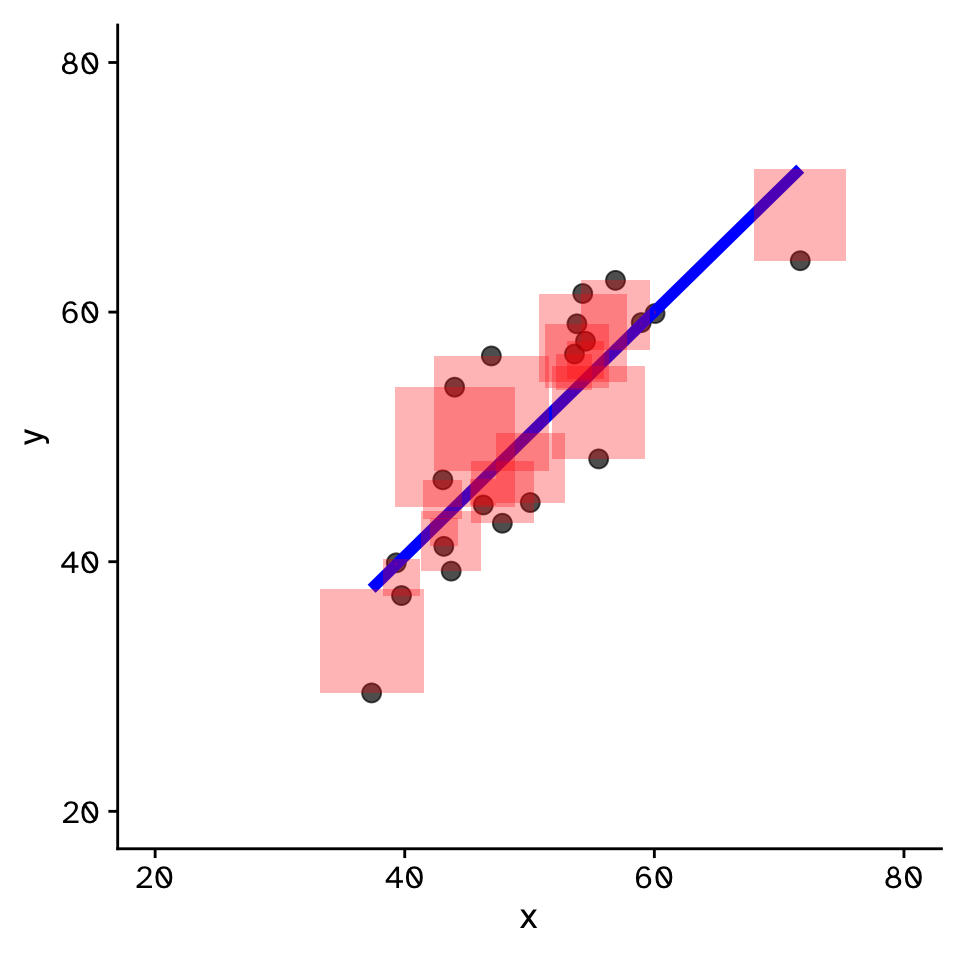
Regression
How does variable Y depend on variable X
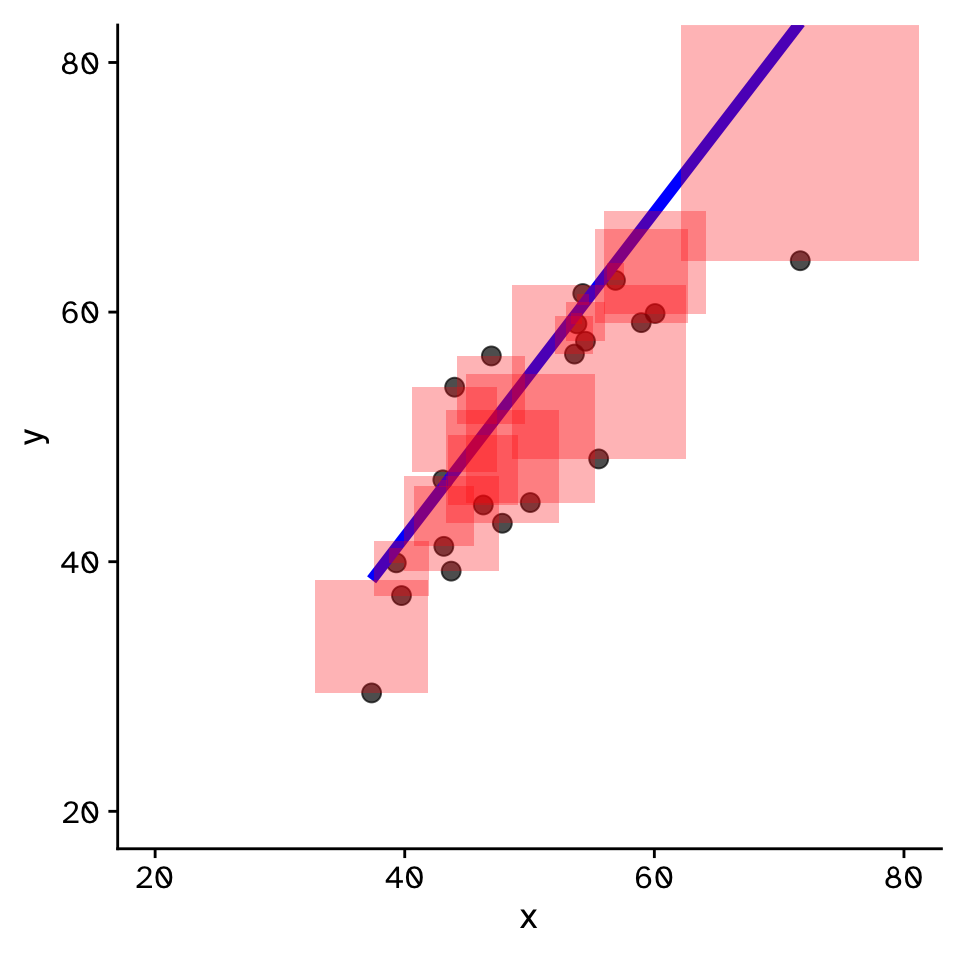
Regression
How does variable Y depend on variable X
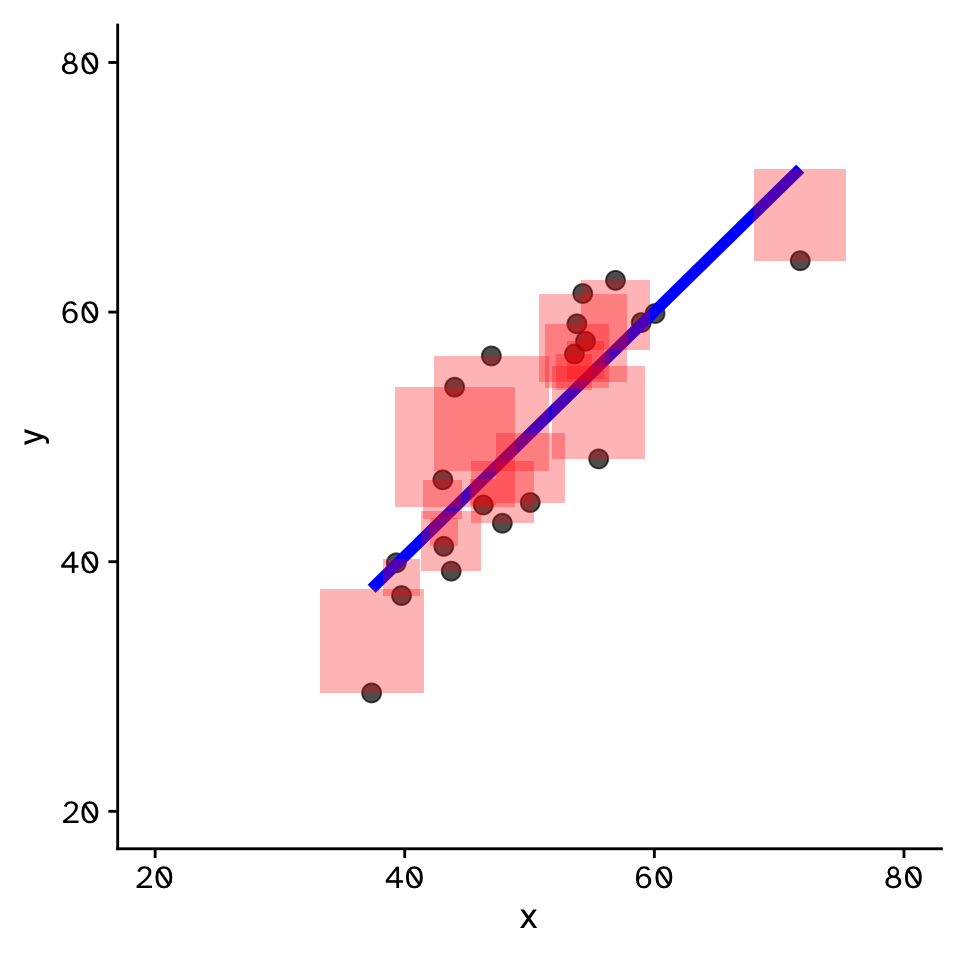
- Fit by solving to minimise the sum of the squared residuals (SSR)
- Find \(\beta_1\) and \(\beta_0\) that minimise the SSR
- Called a “loss function”
- Many approaches to do this!
Regression
How does variable Y depend on variable X
Regression
How to fit in R?
Base R:
Regression
How to fit in R?
With infer:
Regression
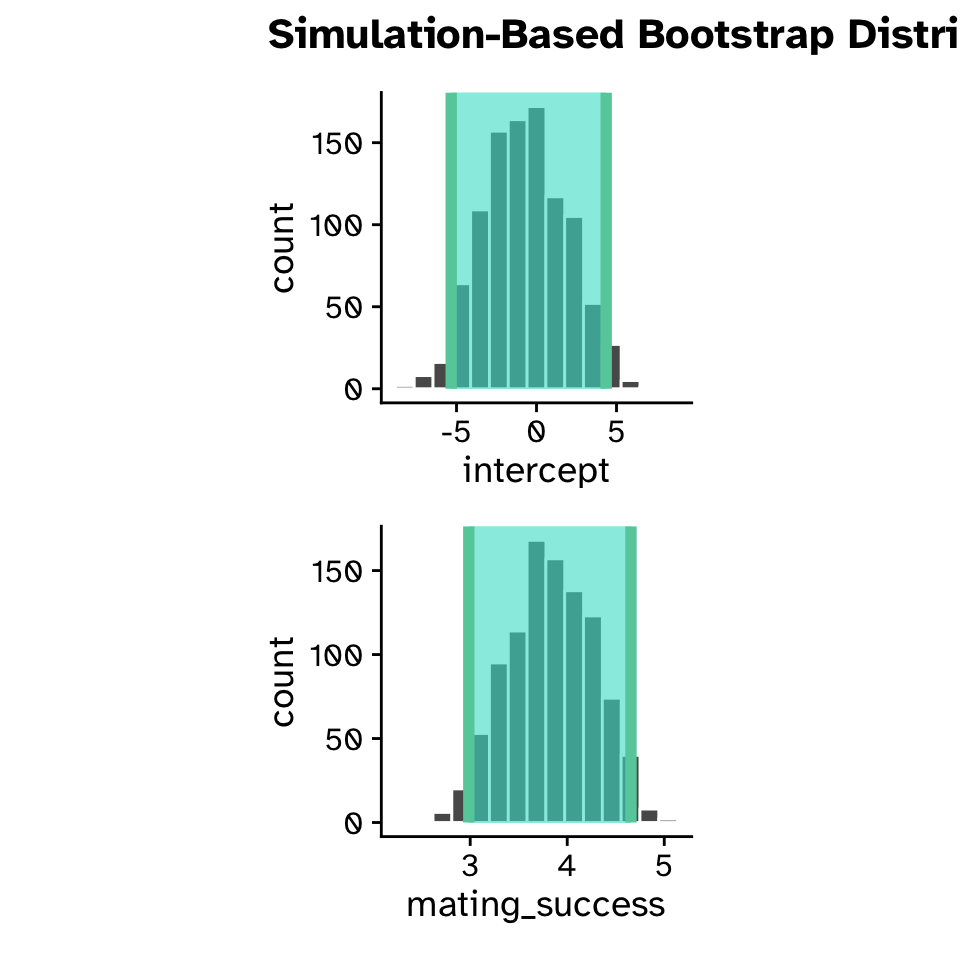
Confidence intervals
boot_dist <-
mating_data |>
specify(reproductive_success ~ mating_success) |>
generate(reps = 1000, type = "bootstrap") |>
fit()
boot_dist# A tibble: 2,000 × 3
# Groups: replicate [1,000]
replicate term estimate
<int> <chr> <dbl>
1 1 intercept -3.75
2 1 mating_success 4.32
3 2 intercept -4.96
4 2 mating_success 4.73
5 3 intercept -0.267
6 3 mating_success 3.80
7 4 intercept 6.72
8 4 mating_success 2.84
9 5 intercept -1.08
10 5 mating_success 3.96
# ℹ 1,990 more rowsRegression
Confidence intervals
Regression
Confidence intervals
Regression
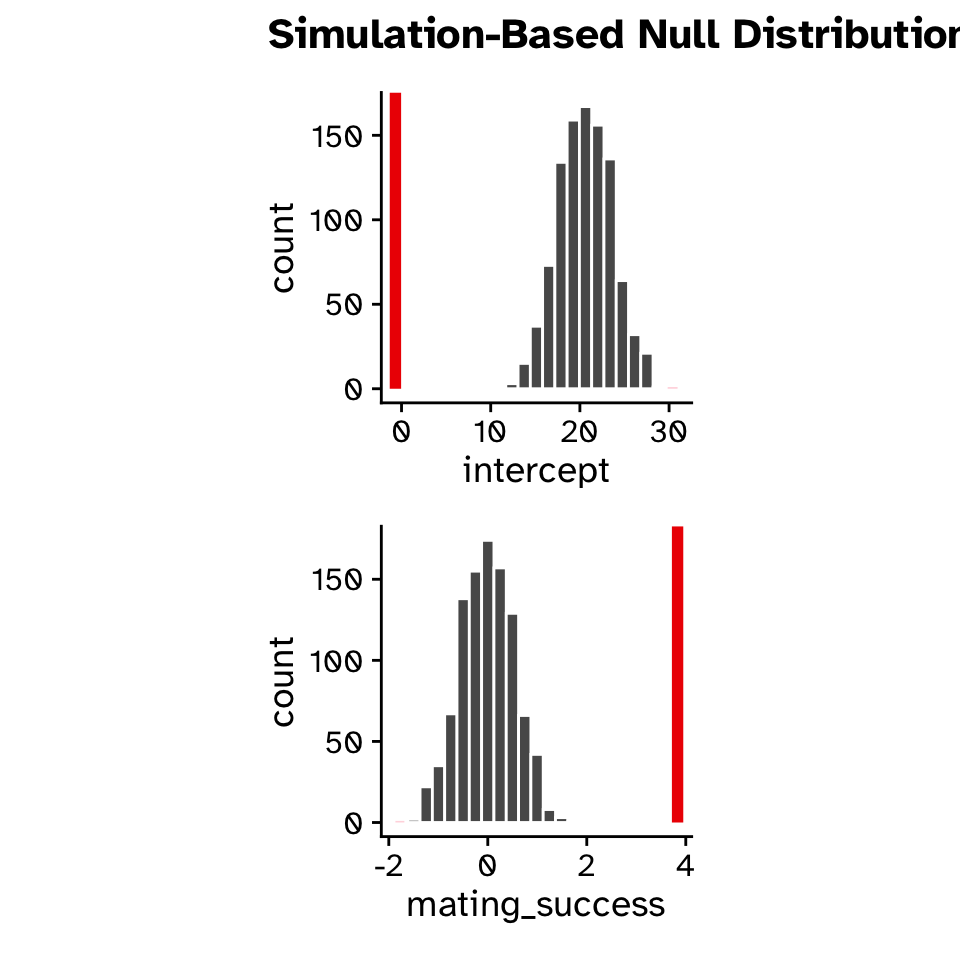
Hypothesis test
- Null hypothesis:
- Slope = 0
- Alternative hypothesis:
- Slope \(\neq\) 0
- Slope < 0
- Slope > 0
Regression
Hypothesis test
null_dist <-
mating_data |>
specify(reproductive_success ~ mating_success) |>
hypothesize(null = "independence") |>
generate(reps = 1000, type = "permute") |>
fit()
null_dist# A tibble: 2,000 × 3
# Groups: replicate [1,000]
replicate term estimate
<int> <chr> <dbl>
1 1 intercept 20.3
2 1 mating_success 0.0382
3 2 intercept 23.9
4 2 mating_success -0.603
5 3 intercept 25.8
6 3 mating_success -0.951
7 4 intercept 23.7
8 4 mating_success -0.570
9 5 intercept 27.2
10 5 mating_success -1.20
# ℹ 1,990 more rowsRegression
Hypothesis test
Regression
Hypothesis test
Regression
Multiple regression
\[ y = \beta_1x+\beta_0 \]
\[ y = \beta_0+\beta_1x+\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5 \]
Take-away points
- Introduced two new methods of generating a null hypothesis
"permute""draw"
- Introduced four new statistics
"F-statistic"(compare variances to infer if means differ)"Chi-sq"(compare distributions of categorical data)"correlation"(do two variables covary linearly?)- Regression coefficients (via
fit())